
分析 根据向量的数量积的运算法则计算即可.
解答 解:∵△ABC是等边三角形,|AB|=2,
∴$\overrightarrow{AB}$•$\overrightarrow{BC}$=-$\overrightarrow{AB}$•$\overrightarrow{CB}$=-|$\overrightarrow{AB}$|•|$\overrightarrow{CB}$|•cosB=-2×2×cos60°=-2,
∴($\overrightarrow{AB}$+$\overrightarrow{AC}$)•$\overrightarrow{BD}$=($\overrightarrow{AB}$+$\overrightarrow{AC}$)•$\frac{1}{2}$$\overrightarrow{BC}$=$\frac{1}{2}$$\overrightarrow{AB}$•$\overrightarrow{BC}$+$\frac{1}{2}$$\overrightarrow{AC}$•$\frac{1}{2}$$\overrightarrow{BC}$=-$\frac{1}{2}$$\overrightarrow{BA}$•$\overrightarrow{BC}$+$\frac{1}{2}$$\overrightarrow{AC}$•$\frac{1}{2}$$\overrightarrow{BC}$=-$\frac{1}{2}$|$\overrightarrow{BA}$|•|$\overrightarrow{BC}$|cos60°+$\frac{1}{2}$|$\overrightarrow{AC}$|•|$\frac{1}{2}$$\overrightarrow{BC}$|cos60°=0
点评 本题考查了向量的数量积的运算法则,属于基础题.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 682 | B. | 782 | C. | 786 | D. | 802 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
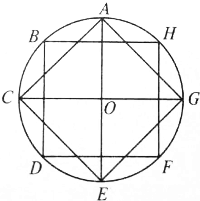 如图所示,A,B,C,D,E,F,G,H是⊙O上的八个等分点,则在以A,B,C,D,E,F,G,H及圆心O这九个点中的任意两点为起点与终点的向量中,模等于半径的向量及模等于半径的$\sqrt{2}$倍的向量分别有( )
如图所示,A,B,C,D,E,F,G,H是⊙O上的八个等分点,则在以A,B,C,D,E,F,G,H及圆心O这九个点中的任意两点为起点与终点的向量中,模等于半径的向量及模等于半径的$\sqrt{2}$倍的向量分别有( )| A. | 8个与8个 | B. | 8个与16个 | C. | 16个与16个 | D. | 16个与8个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 是奇函数 | B. | 是偶函数 | ||
| C. | 既是奇函数又是偶函数 | D. | 既不是奇函数又不是偶函数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com