
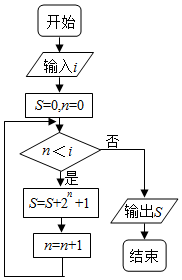
分析 按照程序框图的流程写出前几次循环的结果,据题目对输出s的要求,求出n的最大值,据判断框中n与i的关系求出i的最大值.
解答 解:模拟执行程序,可得
S=0,n=0
若满足条件,n<i,经过第一次循环得到S=2,n=1,
若满足条件,n<i,经过第二次循环得到S=5,n=2,
若满足条件,n<i,经过第三次循环得到S=10,n=3,
若满足条件,n<i,经过第四次循环得到S=19,n=4,
若满足条件,n<i,经过第五次循环得到S=36,n=5,
若满足条件,n<i,经过第六次循环得到S=69,n=6,
∵输出的结果不大于37,
∴n的最大值为4,
∴i的最大值为5.
故答案为:5.
点评 本题主要考查了循环结构,解决程序框图中的循环结构时,常采用写出前几次循环的结果,找规律,属于基础题.


科目:高中数学 来源: 题型:解答题
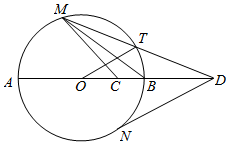 如图,AB是圆O的直径,C是半径OB的中点,D是OB延长线上一点,且BD=OB,直线MD与圆O相交于点M,T(不与A,B重合),DN与圆O相切于点N,连结MC,MB,OT
如图,AB是圆O的直径,C是半径OB的中点,D是OB延长线上一点,且BD=OB,直线MD与圆O相交于点M,T(不与A,B重合),DN与圆O相切于点N,连结MC,MB,OT查看答案和解析>>
科目:高中数学 来源: 题型:填空题
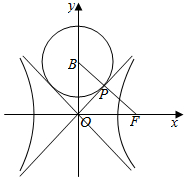 如图,双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a,b>0)虚轴上的端点B(0,b),右焦点F,若以B为圆心的圆与C的一条渐近线相切于点P,且$\overrightarrow{BP}$∥$\overrightarrow{PF}$,则该双曲线的离心率为$\frac{1+\sqrt{5}}{2}$.
如图,双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a,b>0)虚轴上的端点B(0,b),右焦点F,若以B为圆心的圆与C的一条渐近线相切于点P,且$\overrightarrow{BP}$∥$\overrightarrow{PF}$,则该双曲线的离心率为$\frac{1+\sqrt{5}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3}})$ | B. | $({-∞,-\frac{{\sqrt{3}}}{3}})∪({\frac{{\sqrt{3}}}{3},+∞})$ | C. | $[{-\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3}}]$ | D. | $({-∞,-\frac{{\sqrt{3}}}{3}]∪[\frac{{\sqrt{3}}}{3},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
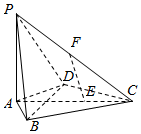 在四棱锥P-ABCD中,PA⊥底面ABCD,AB=AD=2,CB=CD=$\sqrt{7}$,∠BAD=120°,点E在线段AC上,且AE=2EC,F为线段PC的中点.
在四棱锥P-ABCD中,PA⊥底面ABCD,AB=AD=2,CB=CD=$\sqrt{7}$,∠BAD=120°,点E在线段AC上,且AE=2EC,F为线段PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{\frac{11}{3}}$-$\frac{{y}^{2}}{11}$=1 | B. | $\frac{{x}^{2}}{2}$-y2=1 | C. | $\frac{{y}^{2}}{\frac{11}{3}}$-$\frac{{x}^{2}}{11}$=1 | D. | $\frac{{y}^{2}}{11}$-$\frac{{x}^{2}}{\frac{11}{3}}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$±\frac{1}{2}x$ | B. | y=±x | C. | y=±2x | D. | y=±$\sqrt{2}x$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 48 | B. | 24 | C. | 20 | D. | 12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com