
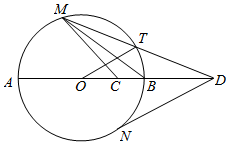
 如图,AB是圆O的直径,C是半径OB的中点,D是OB延长线上一点,且BD=OB,直线MD与圆O相交于点M,T(不与A,B重合),DN与圆O相切于点N,连结MC,MB,OT
如图,AB是圆O的直径,C是半径OB的中点,D是OB延长线上一点,且BD=OB,直线MD与圆O相交于点M,T(不与A,B重合),DN与圆O相切于点N,连结MC,MB,OT分析 (1)利用切割弦定理求得DT•DM=DB•DA,再由圆的半径间的关系得到DB•DA=DO•DC,等量代换得答案;
(2)由(1)结合∠TDO=∠CDM,得到△DTO∽△DCM,则有∠DOT=∠DMC.最后根据圆周角定理得∠DOT的大小.
解答  证明:(1)∵MD与圆O相交于点T
证明:(1)∵MD与圆O相交于点T
∴由切割线定理DN2=DT•DM,DN2=DB•DA,
得DT•DM=DB•DA,
设半径OB=r(r>0),
∵BD=OB,且$BC=OC=\frac{r}{2}$,
∴DB•DA=r•3r=3r2,$DO•DC=2r•\frac{3r}{2}=3{r^2}$,
∴DT•DM=DO•DC,
则$\frac{DT}{DO}=\frac{DC}{DM}$;
(2)由(1)可知,DT•DM=DO•DC,且∠TDO=∠CDM,
故△DTO∽△DCM,
∴∠DOT=∠DMC.
根据圆周角定理得,∠DOT=2∠DMB,则∠BMC=∠DMB=40°,
∴∠DOT=80°.
点评 本题考查与圆有关的比例线段,考查了切割弦定理的应用,训练了三角形相似的判定方法,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
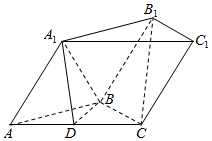 如图,三棱柱ABC-A1B1C1中,平面AA1B1B⊥平面ABC,D是AC的中点.
如图,三棱柱ABC-A1B1C1中,平面AA1B1B⊥平面ABC,D是AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\sqrt{5}$ | D. | $\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | e1>e2 | B. | e1<e2 | C. | e1≤e2 | D. | e1≥e2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com