
| A. | 向左平移$\frac{π}{12}$个单位 | B. | 向右平移$\frac{π}{4}$个单位 | ||
| C. | 向左平移$\frac{π}{4}$个单位 | D. | 向右平移$\frac{3π}{4}$个单位 |
分析 函数$f(x)=Asin(ωx+\frac{π}{4})(ω>0)$的图象与x轴交点的横坐标构成一个公差为$\frac{π}{3}$的等差数列,可知周期T=$\frac{2π}{3}$,可得ω的值,根据三角函数的平移变换规律可得结论.
解答 解:由题意,函数$f(x)=Asin(ωx+\frac{π}{4})(ω>0)$的图象与x轴交点的横坐标构成一个公差为$\frac{π}{3}$的等差数列,可知周期T=$\frac{2π}{3}$,
那么:ω=$\frac{2π}{T}=2π×\frac{3}{2π}=3$.
则f(x)=Asin(3x+$\frac{π}{4}$)=Asin3(x+$\frac{π}{12}$)
要得到g(x)=Acos3x,
即Acos3x=Asin(3x+$\frac{π}{2}$)=Asin3(x+$\frac{π}{6}$)
由题意:可得:f(x)向左平移$\frac{π}{12}$可得g(x)
故选A
点评 本题主要考查函数y=Asin(ωx+∅)的图象变换规律,比较基础.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
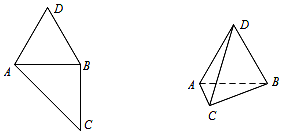 如图,四边形ABCD中,△ABD是正三角形,△ABC是等腰直角三角形,∠ABC=90°,沿AB将△ABD折起,使得平面ABD⊥平面ABC,若三棱锥D-ABC的外接球的表面积为$\frac{28π}{3}$,则三棱锥D-ABC的侧面ACD的面积为$\sqrt{7}$.
如图,四边形ABCD中,△ABD是正三角形,△ABC是等腰直角三角形,∠ABC=90°,沿AB将△ABD折起,使得平面ABD⊥平面ABC,若三棱锥D-ABC的外接球的表面积为$\frac{28π}{3}$,则三棱锥D-ABC的侧面ACD的面积为$\sqrt{7}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com