Question

9．若正方形ABCD的边长为1，且$\overrightarrow{AB}=\overrightarrow a，\overrightarrow{BC}=\overrightarrow b，\overrightarrow{AC}$=$\overrightarrow c$，则$|{3\overrightarrow a+2\overrightarrow b-6\overrightarrow c}$|=5．

Answer 1

分析 可画出图形，而根据$|3\overrightarrow{a}+2\overrightarrow{b}-6\overrightarrow{c}|$=$\sqrt{（3\overrightarrow{a}+2\overrightarrow{b}-6\overrightarrow{c}）^{2}}$进行数量积的计算即可求得答案．

解答 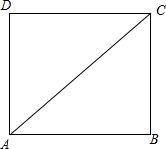解：如图，
$|3\overrightarrow{a}+2\overrightarrow{b}-6\overrightarrow{c}|=\sqrt{（3\overrightarrow{a}+2\overrightarrow{b}-6\overrightarrow{c}）^{2}}$=$\sqrt{9{\overrightarrow{a}}^{2}+4{\overrightarrow{b}}^{2}+36{\overrightarrow{c}}^{2}+12\overrightarrow{a}•\overrightarrow{b}-36\overrightarrow{a}•\overrightarrow{c}-24\overrightarrow{b}•\overrightarrow{c}}$=$\sqrt{9+4+72+0-36-24}=5$．
故答案为：5．

点评 考查求向量长度的方法：|$\overrightarrow{a}$|=$\sqrt{{\overrightarrow{a}}^{2}}$，以及数量积的计算公式．