考点:直线与平面平行的判定,空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:(1)连B1C利用中位线的性质推断出OD∥B1C,进而根据线面平行的判定定理证明出OD∥平面BB1C1C.
(2)先利用线面垂直的性质判断出CC1⊥AC,进而根据线面垂直的判定定理证明出AC⊥平面BB1C1C,进而可知AC⊥MB.利用证明△BCD∽△B1BC,推断出∠CBM=∠BB1C,推断出BM⊥B1C,最后利用线面垂直的判定定理证明出BM⊥平面AB1C,进而可知BM⊥AB1.
解答:
证明:(1)连B
1C,∵O为AB
1中点,D为AC中点,
∴OD∥B
1C,
又B
1C?平面BB
1C
1C,OD?平面BB
1C
1C,
∴OD∥平面BB
1C
1C.
(2)连接B
1C,
∵直三棱柱ABC-A
1B
1C
1,∴CC
1⊥平面ABC
AC?平面ABC,
∴CC
1⊥AC,
又AC⊥BC,CC
1,BC?平面BB
1C
1C,
∴AC⊥平面BB
1C
1C,BM?平面BB
1C
1C,
∴AC⊥MB.
在Rt△BCM与Rt△B
1BC中,
=
=
,
∴△BMC∽△B
1BC,
∴∠CBM=∠BB
1C,
∴∠BB
1C+∠B
1BM=∠CBM+∠B
1BM=90°,
∴BM⊥B
1C,
AC,B
1C?平面AB
1C,
∴BM⊥AB
1C,
∵AB
1?平面AB
1C,
∴BM⊥AB
1.
点评:本题主要考查了线面平行和线面垂直的判定定理的应用.证明线线平行和线线垂直是解题的关键.

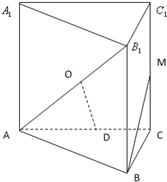 已知直三棱柱ABC-A1B1C1的底面△ABC中,∠C=90°,BC=
已知直三棱柱ABC-A1B1C1的底面△ABC中,∠C=90°,BC=

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 已知平面内一动点P到定点F(2,0)的距离与点P到y轴的距离的差等于2.
已知平面内一动点P到定点F(2,0)的距离与点P到y轴的距离的差等于2.