
| A�� | [$\frac{��}{3}$��$\frac{��}{2}$] | B�� | [$\frac{3��}{4}$��$\frac{5��}{6}$] | C�� | [$\frac{2��}{3}$���� | D�� | [$\frac{2��}{3}$��$\frac{5��}{6}$] |
���� ������������������������ε������ʽ���г�����ʽ������������нǵķ�Χ��
��� �⣺�ߡ�ABC�����S��ABC��[$\frac{\sqrt{3}}{2}$��$\frac{3\sqrt{3}}{2}$]��
��S��ABC=$\frac{1}{2}\left|\overrightarrow{AB}\right|\left|\overrightarrow{BC}\right|sinB$=$\frac{1}{2}$•$\frac{\overrightarrow{AB}•\overrightarrow{BC}}{cos����-B��}$•sinB=$-\frac{3tanB}{2}$��[$\frac{\sqrt{3}}{2}$��$\frac{3\sqrt{3}}{2}$]��
�ɵ�tanB��$[-\sqrt{3}��-\frac{\sqrt{3}}{3}]$����B��[$\frac{2��}{3}$��$\frac{5��}{6}$]��
��ѡ��D��
���� ���⿼����������������ʽ�����������ε������ʽ����������Dz���ʽ��������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -3 | B�� | 3 | C�� | -6 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
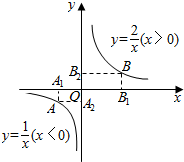 ��ͼ������A�ں���y=$\frac{1}{x}$��x��0����ͼ���ϣ�����B�ں���y=$\frac{2}{x}$��x��0����ͼ���ϣ�����A��B�ֱ���x�ᡢy�������ߣ�����ֱ�ΪA1��A2��B1��B2����|A1B1|=4����|A2B2|����СֵΪ$\frac{3+2\sqrt{2}}{4}$��
��ͼ������A�ں���y=$\frac{1}{x}$��x��0����ͼ���ϣ�����B�ں���y=$\frac{2}{x}$��x��0����ͼ���ϣ�����A��B�ֱ���x�ᡢy�������ߣ�����ֱ�ΪA1��A2��B1��B2����|A1B1|=4����|A2B2|����СֵΪ$\frac{3+2\sqrt{2}}{4}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=1��y=$\frac{x}{x}$ | B�� | y=x��y=$\root{3}{{x}^{3}}$ | ||
| C�� | y=$\sqrt{x-1}$��$\sqrt{x+1}$��y=$\sqrt{{x}^{2}-1}$ | D�� | y=|x|��$y={��{\sqrt{x}}��^2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{2\sqrt{3}}}{3}$ | B�� | $\frac{{2\sqrt{6}}}{3}$ | C�� | $\frac{{\sqrt{3}}}{3}$ | D�� | $\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com