Question

9．已知动点P（x，y）在椭圆$\frac{x^2}{25}$+$\frac{y^2}{16}$=1上，过坐标原点的直线BC与椭圆相交，交点为B，C，点Q是三角形PBC的重心，若点A的坐标为（3，0），|${\overrightarrow{AM}}$|=1，$\overrightarrow{QM}$•$\overrightarrow{AM}$=0，则|${\overrightarrow{QM}}$|的最小值是$\frac{{\sqrt{7}}}{3}$．

Answer 1

分析 由题意画出图形，把求|${\overrightarrow{QM}}$|的最小值转化为求|$\overrightarrow{QA}$|的最小值，再数形结合得答案．

解答 解：如图，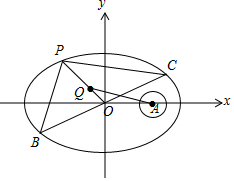
∵|${\overrightarrow{AM}}$|=1，∴M在以A（3，0）为圆心，以1为半径的圆上，
又$\overrightarrow{QM}$•$\overrightarrow{AM}$=0，∴△QMA是以∠QMA为直角的直角三角形，
∴要使|${\overrightarrow{QM}}$|最小，则|$\overrightarrow{QA}$|最小，即O、Q、A共线且Q、A在O的同侧，此时P与椭圆右顶点重合，
∵点Q是三角形PBC的重心，∴|OQ|=$\frac{1}{3}a=\frac{5}{3}$，
则$|\overrightarrow{QA}{|}_{min}=3-\frac{5}{3}=\frac{4}{3}$，∴$|\overrightarrow{QM}{|}_{min}=\sqrt{（\frac{4}{3}）^{2}-{1}^{2}}=\frac{\sqrt{7}}{3}$．
故答案为：$\frac{{\sqrt{7}}}{3}$．

点评 本题考查椭圆的简单性质，考查数形结合的解题思想方法和数学转化思想方法，是中档题．