
分析 取线段AB的中点为D,则由题意可得CD⊥AB,则$\overrightarrow{AC}$•$\overrightarrow{AB}$=$\frac{1}{2}$AB2.故当弦长AB最大(为圆的直径)时,$\overrightarrow{AC}$•$\overrightarrow{AB}$最大,由此求得$\overrightarrow{AC}$•$\overrightarrow{AB}$的最大值.
解答 解:取线段AB的中点为D,则由题意可得CD⊥AB,则$\overrightarrow{AC}$•$\overrightarrow{AB}$=|$\overrightarrow{AB}$|•|$\overrightarrow{AD}$|=$\frac{1}{2}$•${\overrightarrow{AB}}^{2}$=$\frac{1}{2}$AB2.
故当弦长AB最大时,$\overrightarrow{AC}$•$\overrightarrow{AB}$最大,即当圆心C(-2,1)在直线l:x+y+m=0上时,$\overrightarrow{AC}$•$\overrightarrow{AB}$最大.
把圆心C(-2,1)代入直线l:x+y+m=0,求得m=1,
故$\overrightarrow{AC}$•$\overrightarrow{AB}$的最大值为 $\frac{1}{2}$AB2=$\frac{1}{2}$(2r)2=2r2=2×4=8,
故答案为:8.
点评 本题主要考查直线和圆相交的性质,两个向量的数量积的定义,体现了转化的数学思想,属于基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2016-2017学年安徽六安一中高二上文周末检测三数学试卷(解析版) 题型:选择题
若数列的前4项为1,0,1,0,则这个数列的通项公式不可能是( )
A.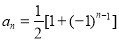
B.
C.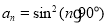
D.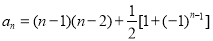
查看答案和解析>>
科目:高中数学 来源:2017届辽宁庄河市高三9月月考数学(理)试卷(解析版) 题型:选择题
某几何体三视图如图所示,则该几何体的体积为(俯视图中弧线是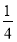 圆弧)( )
圆弧)( )

A. B.
B.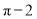
C.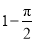 D.
D.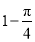
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1)(2) | B. | (1)(3) | C. | (2)(3) | D. | (1)(2)(3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组编号 | 年龄分组 | 球迷 | 所占比例 |
| 1 | [20,25] | 1200 | 0.5 |
| 2 | [25,30] | 1800 | 0.6 |
| 3 | [30,35] | 1000 | 0.5 |
| 4 | [35,40] | a | 0.4 |
| 5 | [40,45] | 300 | 0.2 |
| 6 | [45,50] | 200 | 0.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=$\frac{π}{2}$ | B. | x=π | C. | x=$\frac{π}{6}$ | D. | x=$\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com