
分析 求出曲线的参数方程,则$\frac{y}{x-1}$表示去上的点与(1,0)连线的斜率.求出过点(1,0)的曲线的切线斜率即为$\frac{y}{x-1}$的最值.
解答 解:曲线的普通方程为(x+1)2+y2=1,
过点A(1,0)作圆(x+1)2+y2=1的切线,设切线的斜率为k,
则切线方程为y=kx-k,即kx-y-k=0.
∴圆心(-1,0)到切线的距离d=$\frac{|2k|}{\sqrt{{k}^{2}+1}}$=1,解得k=$±\frac{\sqrt{3}}{3}$.
∵P在圆上,∴-$\frac{\sqrt{3}}{3}$≤kPA≤$\frac{\sqrt{3}}{3}$.即-$\frac{\sqrt{3}}{3}$≤$\frac{y}{x-1}$≤$\frac{\sqrt{3}}{3}$.
故答案为:$[-\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3}]$.
点评 本题考查了参数方程与普通方程的转化,


科目:高中数学 来源: 题型:选择题
| A. | {x|x≥0} | B. | {x|x≤1} | C. | {x|0<x<1} | D. | {x|0≤x≤1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (16,0,4) | B. | (8,0,4) | C. | (8,16,4) | D. | (8,-16,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{8}$ | B. | $\frac{6}{7}$ | C. | $\frac{5}{6}$ | D. | $\frac{36}{49}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
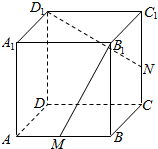 如图所示,在正方体ABCD-A1B1C1D1中,M,N分别是线段AB,CC1的中点,∨MB1P的顶点P在棱CC1与棱C1D1上运动,有以下四个命题:
如图所示,在正方体ABCD-A1B1C1D1中,M,N分别是线段AB,CC1的中点,∨MB1P的顶点P在棱CC1与棱C1D1上运动,有以下四个命题:| A. | ① | B. | ①③ | C. | ②③ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0] | B. | [$-\frac{2}{3}$,$\frac{2}{3}$] | C. | (-∞,-$\frac{2}{3}$] | D. | (-∞,-$\frac{2}{3}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com