Question

4．曲线y=x+2与y=x²所围成的封闭图形的面积s=$\frac{9}{2}$．

Answer 1

分析 联立方程组求出积分的上限和下限，结合积分的几何意义即可得到结论联立方程组求出积分的上限和下限，结合积分的几何意义即可得到结论．

解答 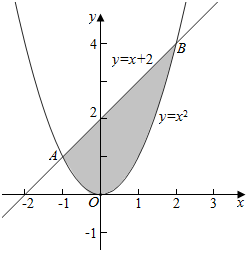解：作出两条曲线对应的封闭区域如图：
由$\left\{\begin{array}{l}{y={x}^{2}}\\{y=x+2}\end{array}\right.$得x²=x+2，即x²-x-2=0，
解得x=-1或x=2，
则根据积分的几何意义可知所求的几何面积S=${∫}_{-1}^{2}$（x+2-x²）dx=（$\frac{1}{3}$x³+$\frac{1}{2}$x²+2x）|${\;}_{-1}^{2}$=$\frac{9}{2}$，
故答案为：

点评 本题主要考查积分的应用，作出对应的图象，求出积分上限和下限，是解决本题的关键．