
分析 直接利用向量的数量积求解即可.
解答 解:向量|$\overrightarrow{a}$|=5,|$\overrightarrow{b}$|=3,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为150°,
则$\overrightarrow{a}$•$\overrightarrow{b}$=|$\overrightarrow{a}$||$\overrightarrow{b}$|cos150°=$-\frac{15\sqrt{3}}{2}$.
故答案为:$-\frac{15\sqrt{3}}{2}$.
点评 本题考查平面斜率的数量积的运算,基本知识的考查.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
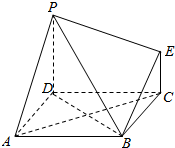 如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且
如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com