
| A. | $\frac{1}{4}$ | B. | $-\frac{1}{5}$ | C. | $-\frac{2}{3}$ | D. | $-\frac{1}{3}$ |
分析 由$k\overrightarrow{a}+\overrightarrow{b}$与$\overrightarrow{a}$垂直,便可得到$(k\overrightarrow{a}+\overrightarrow{b})•\overrightarrow{a}=0$,而根据条件可求出${\overrightarrow{a}}^{2}$和$\overrightarrow{a}•\overrightarrow{b}$的值,从而便可得出k的值.
解答 解:根据条件:$k\overrightarrow{a}+\overrightarrow{b}$与$\overrightarrow{a}$垂直;
∴$(k\overrightarrow{a}+\overrightarrow{b})•\overrightarrow{a}=k{\overrightarrow{a}}^{2}+\overrightarrow{a}•\overrightarrow{b}$=5k+1=0;
∴$k=-\frac{1}{5}$.
故选B.
点评 考查向量垂直的充要条件,以及向量数量积的坐标运算.


科目:高中数学 来源: 题型:选择题
| A. | logab•logbc•logca=1 | B. | 函数f(x)=ex满足f(a+b)=f(a)•f(b) | ||
| C. | 函数f(x)=ex满足f(a•b)=f(a)•f(b) | D. | 若xlog34=1,则4x+4-x=$\frac{10}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
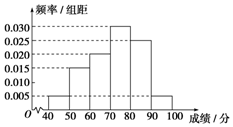 某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图,估计这次测试中数学成绩的平均分、众数、中位数分别是( )
某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图,估计这次测试中数学成绩的平均分、众数、中位数分别是( )| A. | 73.3,75,72 | B. | 72,75,73.3 | C. | 75,72,73.3 | D. | 75,73.3,72 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | .a>c>b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com