考点:棱柱、棱锥、棱台的体积,异面直线及其所成的角
专题:综合题,空间位置关系与距离
分析:(1)利用平移法,确定∠A1CB(或其补角)是异面直线B1C1与A1C所成角,从而可得异面直线B1C1与A1C所成角的大小;
(2)证明A1B1⊥平面B1BCC1,即可四棱锥A1-B1BCC1的体积.
解答:
解:(1)因为B
1C
1∥BC,
所以∠A
1CB(或其补角)是异面直线B
1C
1与A
1C所成角.…(1分)
因为BC⊥AB,BC⊥BB
1,所以BC⊥平面ABB
1,
所以BC⊥A
1B.…(3分)
在Rt△A
1BC中,
tan∠A1CB==,所以
∠A1CB=arctan…(5分)
所以异面直线B
1C
1与A
1C所成角的大小为
arctan. …(6分)
(2)因为A
1B
1⊥B
1C
1,A
1B
1⊥BB
1所以A
1B
1⊥平面B
1BCC
1…(9分)
因为∠ABC=90°,AB=BC=1,BB
1=2,
所以
VA1-B1BCC1=SB1BCC1×A1B1=…(12分)
点评:本题考查异面直线及其所成的角,考查锥体体积的计算,考查学生分析解决问题的能力,属于中档题.

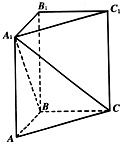 在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=1,BB1=2,求:
在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=1,BB1=2,求:

 字词句段篇系列答案
字词句段篇系列答案