
分析 (Ⅰ)把a1,a3,a4,a2,a5分别代入E(a1,a2,…,an)=|a1-1|+|a2-2|+…+|an-n|进行解答即可;
(Ⅱ)分两种情况进行讨论:当ai=i+1,ai+1=i,aj=j+1,aj+1=j,且{ai,ai+1}∩{aj,aj+1}=∅,其他项ak=k(其中k∉{i,i+1,j,j+1})时和当ai,ai+1,ai+2分别等于i+2,i+1,i或i+1,i+2,i或i+2,i+1,其他项ak=k(其中k∉{i,i+1,i+2});
解答 解:(I)E(1,3,4,2,5)=|1-1|+|3-2|+|4-3|+|2-4|+|5-5|=4;
(II)若数列{an}:a1,a2,…,an的位差和E(a1,a2,…,an)=4,有如下两种情况:
情况一:当ai=i+1,ai+1=i,aj=j+1,aj+1=j,且{ai,ai+1}∩{aj,aj+1}=∅,
其他项ak=k(其中k∉{i,i+1,j,j+1})时,
有(n-3)+(n-4)+…+2+1=$\frac{(n-2)(n-3)}{2}$种可能;
情况二:当ai,ai+1,ai+2分别等于i+2,i+1,i或i+1,i+2,i或i+2,i+1,
其他项ak=k(其中k∉{i,i+1,i+2})时,有3(n-2)种可能;
综上,满足条件的数列{an}:a1,a2,…,an的个数为$\frac{(n-2)(n-3)}{2}$+3(n-2)=$\frac{{({n-2})({n+3})}}{2}$.
故答案为:(I)4;(II)$\frac{{({n-2})({n+3})}}{2}$
点评 本题考查了新定义“位差和”、等差数列的前n项和公式、分类讨论思想方法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,2) | B. | [-1,2) | C. | (-∞,-1] | D. | {-1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
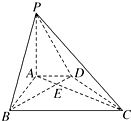 如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=3,AD=2,AB=2$\sqrt{3}$,BC=6.
如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=3,AD=2,AB=2$\sqrt{3}$,BC=6.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F为CE上的一点,且BF⊥平面ACE,AC与BD交于点G.
如图,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F为CE上的一点,且BF⊥平面ACE,AC与BD交于点G.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
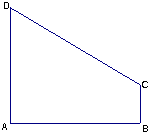 如图,在直角梯形ABCD中,∠BAD=90°,AD∥BC,AB=2,AD=$\frac{3}{2}$,BC=$\frac{1}{2}$,椭圆以A、B为焦点且经过点D.
如图,在直角梯形ABCD中,∠BAD=90°,AD∥BC,AB=2,AD=$\frac{3}{2}$,BC=$\frac{1}{2}$,椭圆以A、B为焦点且经过点D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com