
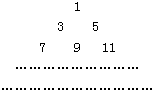
 把正奇数数列{2n-1}中的数按上小下大、左小右大的原则排成如图三角形数表:
把正奇数数列{2n-1}中的数按上小下大、左小右大的原则排成如图三角形数表:分析 (1)三角形数表中前m行共有$1+2+3+…+m=\frac{m(m+1)}{2}$个数,可得:第m行最后一个数应当是所给奇数列中的第$\frac{m(m+1)}{2}$项.故第m行最后一个数是$2•\frac{m(m+1)}{2}-1={m^2}+m-1$.因此,使得amn=2016的m是不等式m2+m-1≥2017的最小正整数解.进而得出n.
(2)由于第n行最后一个数是n2+n-1,且有n个数,若将n2+n-1看成第n行第一个数,则第n行各数成公差为-2的等差数列,故bn=n3.可得$f({b_n})=\frac{n}{2^n}$.再利用“错位相减法”与等比数列的求和公式即可得出.
解答 解:(1)三角形数表中前m行共有$1+2+3+…+m=\frac{m(m+1)}{2}$个数,
∴第m行最后一个数应当是所给奇数列中的第$\frac{m(m+1)}{2}$项.
故第m行最后一个数是$2•\frac{m(m+1)}{2}-1={m^2}+m-1$.
因此,使得amn=2016的m是不等式m2+m-1≥2017的最小正整数解.
由m2+m-1≥2017得m2+m-2018≥0,
∴$m≥\frac{{-1+\sqrt{1+8072}}}{2}>\frac{{-1+\sqrt{7921}}}{2}=\frac{-1+89}{2}=44$,∴m=45.
于是,第45行第一个数是442+44-1+2=1981,∴$n=\frac{2017-1981}{2}+1=19$.
(2)∵第n行最后一个数是n2+n-1,且有n个数,若将n2+n-1看成第n行第一个数,
则第n行各数成公差为-2的等差数列,故${b_n}=n({n^2}+n-1)+\frac{n(n-1)}{2}(-2)={n^3}$.
∴$f({b_n})=\frac{n}{2^n}$.
故${S_n}=\frac{1}{2}+\frac{2}{2^2}+\frac{3}{2^3}+…+\frac{n-1}{{{2^{n-1}}}}+\frac{n}{2^n}$.
∴$\frac{1}{2}{S_n}=\frac{1}{2^2}+\frac{2}{2^3}+\frac{3}{2^4}+…+\frac{n-1}{2^n}+\frac{n}{{{2^{n+1}}}}$,
两式相减得:$\frac{1}{2}{S_n}=\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+…+\frac{1}{2^n}-\frac{n}{{{2^{n+1}}}}$=$\frac{{\frac{1}{2}({1-\frac{1}{2^n}})}}{{1-\frac{1}{2}}}-\frac{n}{{{2^{n+1}}}}=1-\frac{1}{2^n}-\frac{n}{{{2^{n+1}}}}$.
∴${S_n}=2-\frac{n+2}{2^n}$.
点评 本题考查了等差数列与等比数列的通项公式及其求和公式、“错位相减法”,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
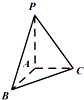
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com