
分析 根据题意,结合函数的奇偶性与单调性,原不等式f(x)>0可以转化为|x|<1且x≠0,解可得x的取值范围,即可得答案.
解答 解:根据题意,对于函数f(x),f(1)=0,则f(x)>0?f(x)>f(1),
又由函数f(x)为偶函数,则f(x)>f(1)?f(|x|)>f(1),
函数f(x)在(0,+∞)单调递减,则f(|x|)>f(1)?|x|<1且x≠0,
综合可得:f(x)>0?|x|<1且x≠0,
解可得-1<x<1且x≠0,
即不等式f(x)>0的解集为(-1,0)∪(0,1);
故答案为:(-1,0)∪(0,1).
点评 本题考查函数单调性与奇偶性的综合应用,关键是综合运用函数的奇偶性与单调性分析,得到关于x的不等式.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ac>bc | B. | ac>bc | C. | loga(a-c)>logb(b-c) | D. | $\frac{a}{a-c}$>$\frac{b}{b-c}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
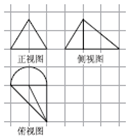 如图,在各小正方形边长为1的网格上依次为某几何体的正视图.侧视图与俯视图,其中正视图为等边三角形,则此几何体的体积为( )
如图,在各小正方形边长为1的网格上依次为某几何体的正视图.侧视图与俯视图,其中正视图为等边三角形,则此几何体的体积为( )| A. | 1+$\frac{2π}{3}$ | B. | $\frac{4}{3}$+$\frac{2π}{3}$ | C. | $\frac{2\sqrt{3}}{3}$+$\frac{\sqrt{3}π}{6}$ | D. | $\frac{2\sqrt{3}}{3}$+$\frac{\sqrt{3}π}{3}$ |
查看答案和解析>>
科目:高中数学 来源:2017届湖南长沙长郡中学高三上周测十二数学(理)试卷(解析版) 题型:解答题
已知向量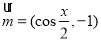 ,
,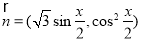 ,函数
,函数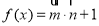 .
.
(1)若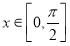 ,
,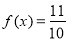 ,求
,求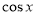 的值;
的值;
(2)在△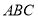 中,角
中,角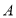 ,
,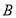 ,
,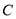 的对边分别是
的对边分别是 ,
,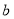 ,
,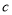 ,且满足
,且满足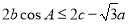 ,求角
,求角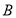 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $x=\frac{π}{6}$ | B. | $x=\frac{π}{3}$ | C. | $x=\frac{2π}{3}$ | D. | $x=\frac{5π}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com