
| A. | (-∞,lge-lg(lge)] | B. | (-∞,1] | C. | [1,lge-lg(lge)] | D. | [lge-lg(lge),+∞) |
分析 将所求变形为a-x≤|lgx|恒成立,结合图象得到满足条件的a.
解答 解:对任意的x>0,总有f(x)=a-x-|lgx|≤0,即a-x≤|lgx|恒成立,设y=-x+a,g(x)=|lgx|,如图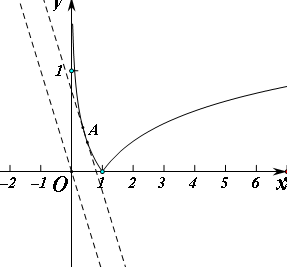 当直线y=-x+a与g(x)相切时是a的最大值时,设切点为A(x,y),
当直线y=-x+a与g(x)相切时是a的最大值时,设切点为A(x,y),
则-1=(-lgx)',得到x=lge,所以y=-lg(lge),
所以切线方程为:y+lg(lge)=-(x-lge),令x=0得到y=lge-lg(lge),
所以a的取值范围为:(-∞,lge-lg(lge));
故选A.
点评 本题考查了不等式恒成立问题;关键是分解为两个函数图象的位置关系问题,借助于数形结合求得;属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
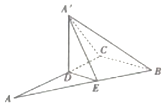 如图,将直角△ABC沿着平行BC边的直线DE折起,使得平面A′DE⊥平面BCDE,其中D、E分别在AC、AB边上,且AC⊥BC,BC=3,AB=5,点A′为点A折后对应的点,当四棱锥A′-BCDE的体积取得最大值时,求AD的长.
如图,将直角△ABC沿着平行BC边的直线DE折起,使得平面A′DE⊥平面BCDE,其中D、E分别在AC、AB边上,且AC⊥BC,BC=3,AB=5,点A′为点A折后对应的点,当四棱锥A′-BCDE的体积取得最大值时,求AD的长.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\sqrt{13}$ | C. | $\sqrt{21}$ | D. | $\sqrt{57}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
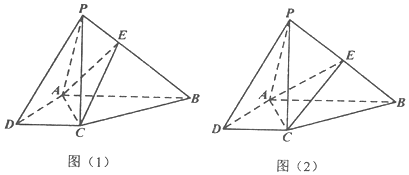
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4:3:2 | B. | 2:3:4 | C. | $\frac{1}{4}$:$\frac{1}{3}$:$\frac{1}{2}$ | D. | $\frac{1}{2}$:$\frac{1}{3}$:$\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
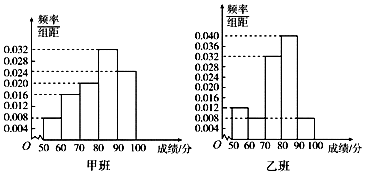
| 甲班(A方式) | 乙班(B方式) | 总计 | |
| 成绩优秀 | 12 | 4 | 20 |
| 成绩不优秀 | 38 | 46 | 80 |
| 总计 | 50 | 50 | 100 |
| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com