
【题目】2018年秋季,我省高一年级全面实行新高考政策,为了调查学生对新政策的了解情况,准备从某校高一![]() 三个班级抽取10名学生参加调查.已知
三个班级抽取10名学生参加调查.已知![]() 三个班级学生人数分别为40人,30人,30人.考虑使用简单随机抽样、分层抽样和系统抽样三种方案,使用简单随机抽样和分层抽样时,将学生按
三个班级学生人数分别为40人,30人,30人.考虑使用简单随机抽样、分层抽样和系统抽样三种方案,使用简单随机抽样和分层抽样时,将学生按![]() 三个班级依次统一编号为1,2,…,100;使用系统抽样,将学生统一编号为1,2,…,100,并将整个编号依次分为10段.如果抽得的号码有下列四种情况:
三个班级依次统一编号为1,2,…,100;使用系统抽样,将学生统一编号为1,2,…,100,并将整个编号依次分为10段.如果抽得的号码有下列四种情况:
①7,17,27,37,47,57,67,77,87,97;②3,9,15,33,43,53,65,75,85,95;
③9,19,29,39,49,59,69,79,89,99,;④2,12,22,32,42,52,62,73,83,96.
关于上述样本的下列结论中,正确的是( )
A. ①③都可能为分层抽样 B. ②④都不能为分层抽样
C. ①④都可能为系统抽样 D. ②③都不能为系统抽样
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:
【题目】边长为2的正三角形ABC中,点D,E,G分别是边AB,AC,BC的中点,连接DE,连接AG交DE于点![]() 现将
现将![]() 沿DE折叠至
沿DE折叠至![]() 的位置,使得平面
的位置,使得平面![]() 平面BCED,连接A1G,EG.
平面BCED,连接A1G,EG.
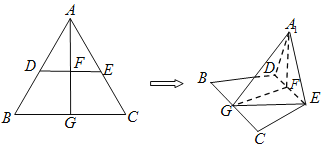
![]() 证明:DE∥平面A1BC
证明:DE∥平面A1BC
![]() 求点B到平面A1EG的距离.
求点B到平面A1EG的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某小区中央广场由两部分组成,一部分是边长为![]() 的正方形
的正方形![]() ,另一部分是以
,另一部分是以![]() 为直径的半圆,其圆心为
为直径的半圆,其圆心为![]() .规划修建的
.规划修建的![]() 条直道
条直道![]() ,
, ![]() ,
, ![]() 将广场分割为
将广场分割为![]() 个区域:Ⅰ、Ⅲ、Ⅴ为绿化区域(图中阴影部分),Ⅱ、Ⅳ、Ⅵ为休闲区域,其中点
个区域:Ⅰ、Ⅲ、Ⅴ为绿化区域(图中阴影部分),Ⅱ、Ⅳ、Ⅵ为休闲区域,其中点![]() 在半圆弧上,
在半圆弧上, ![]() 分别与
分别与![]() ,
, ![]() 相交于点
相交于点![]() ,
, ![]() .(道路宽度忽略不计)
.(道路宽度忽略不计)
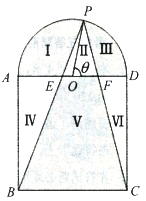
(1)若![]() 经过圆心,求点
经过圆心,求点![]() 到
到![]() 的距离;
的距离;
(2)设![]() ,
, ![]() .
.
①试用![]() 表示
表示![]() 的长度;
的长度;
②当![]() 为何值时,绿化区域面积之和最大.
为何值时,绿化区域面积之和最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 同时满足:①对于任意的正整数
同时满足:①对于任意的正整数![]() ,
, ![]() 恒成立;②对于给定的正整数
恒成立;②对于给定的正整数![]() ,
, ![]() 对于任意的正整数
对于任意的正整数![]() 恒成立,则称数列
恒成立,则称数列![]() 是“
是“![]() 数列”.
数列”.
(1)已知![]() 判断数列
判断数列![]() 是否为“
是否为“![]() 数列”,并说明理由;
数列”,并说明理由;
(2)已知数列![]() 是“
是“![]() 数列”,且存在整数
数列”,且存在整数![]() ,使得
,使得![]() ,
, ![]() ,
, ![]() ,
, ![]() 成等差数列,证明:
成等差数列,证明: ![]() 是等差数列.
是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为研究学生的身体素质与与课外体育锻炼时间的关系,对该校200名高三学生的课外体育锻炼平均每天运动的时间进行调查,如下表:(平均每天锻炼的时间单位:分钟)
将学生日均课外体育运动时间在![]() 上的学生评价为“课外体育达标”.
上的学生评价为“课外体育达标”.
平均每天锻炼的时间(分钟) |
|
|
|
|
|
|
总人数 | 20 | 36 | 44 | 50 | 40 | 10 |
请根据上述表格中的统计数据填写下面![]() 列联表,并通过计算判断是否能在犯错误的概率不超过
列联表,并通过计算判断是否能在犯错误的概率不超过![]() 的前提下认为“课外体育达标”与性别有关?
的前提下认为“课外体育达标”与性别有关?
课外体育不达标 | 课外体育达标 | 合计 | |
男 | |||
女 | 20 | 110 | |
合计 |
从上述200名学生中,按“课外体育达标”、“课外体育不达标”分层抽样,抽取4人得到一个样本,再从这个样本中抽取2人,求恰好抽到一名“课外体育不达标”学生的概率.
参考公式:![]() ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com