
分析 (1)根据相互独立事件的概率乘法公式,求得该网民三种商品都买的概率.
(2)分类讨论,求得该网民至少购买2种商品的概率.
解答 解:(1)由题意可得,该网民三种商品都买的概率为$\frac{3}{4}•\frac{2}{3}•\frac{1}{2}$=$\frac{1}{4}$.
(2)记“该网民购买A种商品”、“该网民购买B种商品”、“该网民购买C种商品”分别为事件Ai,i=2,3,
则该网民至少购买2种商品的概率为 P(A1A2$\overline{{A}_{3}}$+A1A3$\overline{{A}_{2}}$+$\overline{{A}_{1}}$A2A3+A1A2A3)=P(A1A2$\overline{{A}_{3}}$)+P(A1A3$\overline{{A}_{2}}$)+P($\overline{{A}_{1}}$A2A3)+P(A1A2A3)
=$\frac{3}{4}•\frac{1}{3}•(1-\frac{1}{2})$+$\frac{3}{4}•\frac{1}{2}$•(1-$\frac{2}{3}$)+(1-$\frac{3}{4}$)•$\frac{2}{3}•\frac{1}{2}$+$\frac{3}{4}•\frac{2}{3}•\frac{1}{2}$=$\frac{7}{12}$,
所以,该网民至少购买2种商品的概率为 $\frac{7}{12}$.
点评 本题主要考查相互独立事件的概率乘法公式的应用,事件和它的对立事件概率间的关系,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}或-\frac{4}{3}$ | B. | -$\frac{4}{3}$ | C. | -$\frac{3}{4}$ | D. | $\frac{3}{4}或-\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -7 | B. | -1 | C. | $\frac{13}{3}$ | D. | -1或-7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
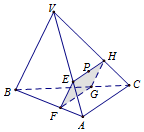 如图所示,在四面体VABC木块中,P为△VAC的重心,这点P作截面EFGH,若截面EFGH是平行四边形,则该截面把木块分成两部分体积之比为$\frac{7}{20}$. (埴体积小与体积大之比)
如图所示,在四面体VABC木块中,P为△VAC的重心,这点P作截面EFGH,若截面EFGH是平行四边形,则该截面把木块分成两部分体积之比为$\frac{7}{20}$. (埴体积小与体积大之比)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com