
如图,三棱柱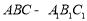 中,
中,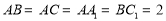 ,
, 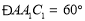 ,平面
,平面 平面
平面 ,
, 与
与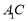 相交于点
相交于点 .
.

(1)求证: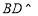 平面
平面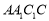 ;
;
(2)设点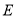 是直线
是直线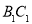 上一点,且
上一点,且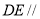 平面
平面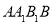 ,求平面
,求平面 与平面
与平面 夹角的余弦值.
夹角的余弦值.
(1)答案见解析;(2)平面 与平面
与平面 夹角的余弦值是
夹角的余弦值是
【解析】
试题分析:(1)已知平面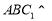 平面
平面 ,若证明线面垂直,需应用面面垂直的性质定理,只需要证明平面
,若证明线面垂直,需应用面面垂直的性质定理,只需要证明平面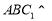 经过平面
经过平面 的垂线,即证:
的垂线,即证: 平面
平面 因为底面
因为底面 为菱形,所以
为菱形,所以 为
为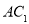 的中点,在
的中点,在 中
中 ,
, 为
为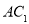 的中点,所以
的中点,所以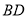 垂直平面
垂直平面 进而得证;(2)过点
进而得证;(2)过点 的直线
的直线 平行平面
平行平面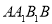 ,过点
,过点 的平面垂直平面
的平面垂直平面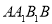 ,显然取
,显然取 中点
中点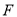 ,显然点
,显然点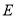 为
为 的中点,由(1)建立空间直角坐标系,进而分别得到两个平面的法向量,利用公式求得面面角的夹角的余弦值.
的中点,由(1)建立空间直角坐标系,进而分别得到两个平面的法向量,利用公式求得面面角的夹角的余弦值.
试题解析:(1)由已知得侧面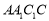 是菱形,
是菱形,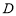 是
是 的中点,
的中点,
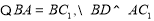 2分
2分
平面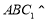 平面
平面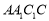 ,且
,且 ,平面
,平面 平面
平面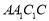 =AC1
=AC1

 平面
平面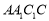 . 4分
. 4分
(2)设点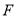 是
是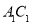 的中点,因为点
的中点,因为点 是
是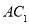 的中点,所以
的中点,所以
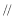 平面
平面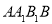 ,
,
又因为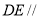 面
面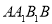 ,所以平面
,所以平面 平面
平面 ,又平面
,又平面 平面
平面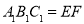 ,
,
平面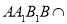 平面
平面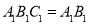 ,所以
,所以 ,所以点
,所以点 是
是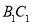 的中点。 6分
的中点。 6分
如图,以 为原点,以
为原点,以 所在直线分别为
所在直线分别为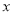 轴,
轴,  轴,z轴建立空间直角坐标系.
轴,z轴建立空间直角坐标系.

由已知可得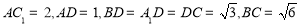 所以
所以
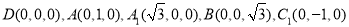 7分
7分
设平面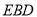 的一个法向量是
的一个法向量是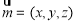 由
由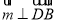 得
得 ,
,
又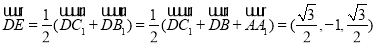
由
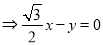
令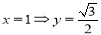 ,所以
,所以 9分
9分
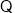 平面
平面 平面
平面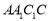 ,
, ,所以
,所以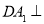 平面
平面 ∴
∴ 是平面
是平面 的一个法向量是
的一个法向量是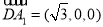 , 10分
, 10分

平面 与平面
与平面 夹角的余弦值是
夹角的余弦值是 12分
12分
考点:1.面面垂直的性质定理;2.线面平行的判定定理;3.向量法求二面角.


科目:高中数学 来源:2014-2015学年江苏省无锡市高三上学期期末考试理科数学试卷(解析版) 题型:解答题
设函数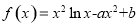 在点
在点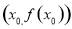 处的切线方程为
处的切线方程为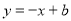 .
.
(1)求实数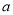 及
及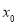 的值;
的值;
(2)求证:对任意实数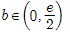 ,函数
,函数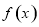 有且仅有两个零点.
有且仅有两个零点.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河南省信阳市毕业班第二次调研检测文科数学试卷(解析版) 题型:选择题
设等差数列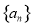 的前
的前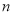 项和为
项和为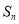 ,若
,若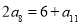 ,则
,则 的值等于( )
的值等于( )
(A) (B)
(B) (C)
(C) (D)
(D)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省济南市高三上学期期末考试理科数学试卷(解析版) 题型:选择题
将函数 的图象向左平移
的图象向左平移 个单位,得到函数
个单位,得到函数 的图象,则
的图象,则 的表达式可以是
的表达式可以是
A. 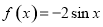 B.
B. 
C. 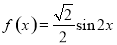 D.
D. 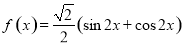
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省南昌市高三上学期第四次月考理科数学试卷(解析版) 题型:解答题
选修4—5:不等式选讲
设不等式 的解集为
的解集为 , 且
, 且 .
.
(Ⅰ) 试比较 与
与 的大小;
的大小;
(Ⅱ) 设 表示数集
表示数集 中的最大数, 且
中的最大数, 且 , 求
, 求 的范围.
的范围.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省南昌市高三上学期第四次月考理科数学试卷(解析版) 题型:选择题
若直线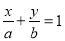 经过点
经过点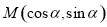 ,则( )
,则( )
A.a2+b2≤1 B.a2+b2≥1 C.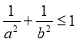 D.
D.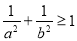
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省宿迁市高三下学期期初开学联考文科数学试卷(解析版) 题型:填空题
已知锐角A,B满足tan(A+B)=2tanA,则tanB的最大值是 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖南省名校高二上学期期末考试文科数学试卷(解析版) 题型:选择题
△ABC的两个顶点为A(-3,0),B(3,0),△ABC周长为16,则顶点C的轨迹方程为( )
A.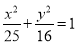 (y≠0) B.
(y≠0) B. 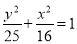 (y≠0)
(y≠0)
C.  (y≠0) D.
(y≠0) D. 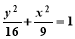 (y≠0)
(y≠0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com