
已知二次函数f(x)=ax2+bx+c的图象与x轴有两个不同的交点,若f(c)=0且0<x<c时,f(x)>0,
(1)证明: 是f(x)=0的一个根;
是f(x)=0的一个根;
(2)试比较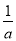 与c的大小;
与c的大小;
(3)证明:-2<b<-1.
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-5直线、平面垂直的判定及性质(解析版) 题型:填空题
如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面各边都相等,M是PC上的一动点,当点M满足________时,平面MBD⊥平面PCD.(只要填写一个你认为是正确的条件即可)

查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-3空间点直线平面之间的位置关系(解析版) 题型:选择题
已知m和n是两条不同的直线,α和β是两个不重合的平面,那么下面给出的条件中一定能推出m⊥β的是( )
A.α⊥β,且m?α B.m∥n,且n⊥β
C.α⊥β,且m∥α D.m⊥n,且n∥β
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-7数学归纳法(解析版) 题型:选择题
用数学归纳法证明1+2+3+…+n2=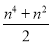 ,则当n=k+1时左端应在n=k的基础上加上( )
,则当n=k+1时左端应在n=k的基础上加上( )
A.k2+1
B.(k+1)2
C.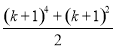
D.(k2+1)+(k2+2)+…+(k+1)2
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-7数学归纳法(解析版) 题型:选择题
用数学归纳法证明“n3+(n+1)3+(n+2)3(n∈N*)能被9整除”,要利用归纳假设证n=k+1时的情况,只需展开( )
A.(k+3)3 B.(k+2)3
C.(k+1)3 D.(k+1)3+(k+2)3
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-6直接证明与间接证明(解析版) 题型:解答题
已知x∈R,a=x2+ ,b=2-x,c=x2-x+1,试证明a,b,c至少有一个不小于1.
,b=2-x,c=x2-x+1,试证明a,b,c至少有一个不小于1.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-6直接证明与间接证明(解析版) 题型:选择题
分析法又称执果索因法,若用分析法证明:“设a>b>c,且a+b+c=0,求证  <
<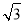 a”索的因应是( )
a”索的因应是( )
A.a-b>0 B.a-c>0
C.(a-b)(a-c)>0 D.(a-b)(a-c)<0
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-4基本不等式(解析版) 题型:选择题
已知b>0,直线(b2+1)x+ay+2=0与直线x-b2y-1=0互相垂直,则ab的最小值等于( )
A.1 B.2 C.2 D.2
D.2
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-1不等关系与不等式(解析版) 题型:选择题
已知a>b>0,给出下列四个不等式:①a2>b2;②2a>2b-1;③ >
>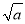 -
- ;④a3+b3>2a2b.
;④a3+b3>2a2b.
其中一定成立的不等式为( )
A.①②③ B.①②④
C.①③④ D.②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com