
分析 先设M(x,y),可讨论l1是否存在斜率:(1)不存在斜率时,可求出A(1,0),B(0,-1),从而由$\overrightarrow{AM}=2\overrightarrow{MB}$可以求出x=$\frac{1}{3},y=-\frac{2}{3}$,即点M($\frac{1}{3},-\frac{2}{3}$),(2)存在斜率时,可设斜率为k,从而可以分别写出直线l1,l2的方程,从而可以求出$A(-\frac{4}{k}+1,0),B(0,\frac{3}{k}-1)$,这样根据$\overrightarrow{AM}=2\overrightarrow{MB}$便可用k分别表示出x,y,这样消去k便可得出关于x,y的方程,并验证点$M(\frac{1}{3},-\frac{2}{3})$是否满足该方程,从而便得出点M的轨迹方程.
解答 解:设M(x,y),
(1)若l1不存在斜率,则:l1垂直x轴,l2垂直y轴;
∴A(1,0),B(0,-1);
∴由$\overrightarrow{AM}=2\overrightarrow{MB}$得,(x-1,y)=2(-x,-1-y);
∴$\left\{\begin{array}{l}{x-1=-2x}\\{y=-2-2y}\end{array}\right.$;
∴$\left\{\begin{array}{l}{x=\frac{1}{3}}\\{y=-\frac{2}{3}}\end{array}\right.$;
即$M(\frac{1}{3},-\frac{2}{3})$;
(2)若l1斜率为k,l2斜率为$-\frac{1}{k}$,则:
l1:y-4=k(x-1),令y=0,x=$-\frac{4}{k}+1$;
∴$A(-\frac{4}{k}+1,0)$;
l2:$y+1=-\frac{1}{k}(x-3)$,令x=0,y=$\frac{3}{k}-1$;
∴$B(0,\frac{3}{k}-1)$;
∴由$\overrightarrow{AM}=2\overrightarrow{MB}$得,$(x+\frac{4}{k}-1,y)=2(-x,\frac{3}{k}-1-y)$;
∴$\left\{\begin{array}{l}{x+\frac{4}{k}-1=-2x}\\{y=\frac{6}{k}-2-2y}\end{array}\right.$;
∴消去k并整理得:9x+6y+1=0;
点$M(\frac{1}{3},-\frac{2}{3})$满足方程9x+6y+1=0;
综(1)(2)知,点M的轨迹方程为9x+6y+1=0.
故答案为:9x+6y+1=0.
点评 考查直线垂直于x轴时不存在斜率,相互垂直的直线的斜率关系,根据点的坐标求向量的坐标,向量坐标的数乘运算,以及直线的点斜式方程,求直线和x,y轴交点的方法,注意不要忘了斜率不存在的情况.


科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | c>b>a | D. | b>c>a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
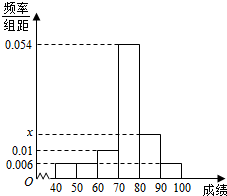 某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].已知图中x=0.018,则由直观图估算出中位数(精确到0.1)的值为( )
某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].已知图中x=0.018,则由直观图估算出中位数(精确到0.1)的值为( )| A. | 75.5 | B. | 75.2 | C. | 75.1 | D. | 75.3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $-\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $-\frac{1}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com