
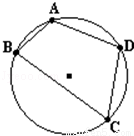
如图,已知圆内接四边形ABCD的边长为AB=2,BC=6,CD=DA=4,则四边形ABCD面积为( )
A.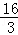 B.8 C.
B.8 C.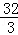 D.8
D.8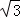
D
【解析】
试题分析:连结BD,可得四边形ABCD的面积S=S△ABD+S△CBD,由圆内接四边形性质、诱导公式和三角形面积公式,化简得S= (AB•AD+BC•CD)sinA=16sinA.再根据△ABD和△CBD有公共边BD,利用余弦定理列式解出cosA的值,从而解得A=120°,代入前面式子即可得出四边形ABCD的面积.
(AB•AD+BC•CD)sinA=16sinA.再根据△ABD和△CBD有公共边BD,利用余弦定理列式解出cosA的值,从而解得A=120°,代入前面式子即可得出四边形ABCD的面积.
【解析】
连结BD,可得四边形ABCD的面积为
S=S△ABD+S△CBD= AB•ADsinA+
AB•ADsinA+ BC•CDsinC
BC•CDsinC
∵四边形ABCD内接于圆,∴A+C=180°,可得sinA=sinC.
S= AB•ADsinA+
AB•ADsinA+ BC•CDsinC
BC•CDsinC
= (AB•AD+BC•CD)sinA=
(AB•AD+BC•CD)sinA= (2×4+6×4)sinA=16sinA.…(*)
(2×4+6×4)sinA=16sinA.…(*)
在△ABD中,由余弦定理可得
BD2=AB2+AD2﹣2AB•ADcosA=22+42﹣2×2×4cosA=20﹣16cosA,
同理可得:在△CDB中,BD2=CB2+CD2﹣2CB•CDcosC=62+42﹣2×6×4cosC=52﹣48cosC,
∴20﹣16cosA=52﹣48cosC
结合cosC=cos(180°﹣A)=﹣cosA,得64cosA=﹣32,解得cosA=﹣ ,
,
∵A∈(0°,180°),∴A=120°,
代入(*)式,可得四边形ABCD面积S=16sin120°=8
故选:D


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:[同步]2015人教A版必修二2.1空间点、直线、平面间位置关系练习卷(解析版) 题型:
与正方体ABCD﹣A1B1C1D1的三条棱AB、CC1、A1D1所在直线的距离相等的点( )
A.有且只有1个 B.有且只有2个 C.有且只有3个 D.有无数个
查看答案和解析>>
科目:高中数学 来源:[同步]2014新人教A版选修4-1 2.3圆的切线性质及判定定理练习(解析版) 题型:选择题
如图,半径为2的两个等圆⊙O1与⊙O2外切于点P,过O1作⊙O2的两条切线,切点分别为A,B,与⊙O1分别交于C,D,则APB与CPD的弧长之和为( )
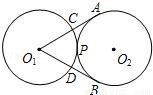
A.2π B.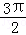 C.π D.
C.π D.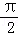
查看答案和解析>>
科目:高中数学 来源:[同步]2014新人教A版选修4-1 2.2圆内接四边形性质与判定定理(解析版) 题型:填空题
(2014•泸州三模)在△ABC中,O是其外接圆的圆心,其两条中线的交点是G,两条高线的交点是H,设OG=λGH,则λ的值为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014新人教A版选修4-1 2.2圆内接四边形性质与判定定理(解析版) 题型:选择题
圆内接四边形ABCD中,AD∥BC,AC与BD交于点E,在下图中全等三角形的对数为( )
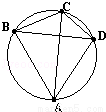
A.2对 B.3对 C.4对 D.5对
查看答案和解析>>
科目:高中数学 来源:[同步]2014新人教A版选修4-1 2.2圆内接四边形性质与判定定理(解析版) 题型:选择题
(2009•成都二模)已知曲线y=2sinx与曲线y=ax2+bx+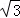 的一个交点P的横坐标为
的一个交点P的横坐标为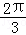 ,且两曲线在交点P处的切线与两坐标轴围成的四边形恰好有外接圆,则a与b的值分别为( )
,且两曲线在交点P处的切线与两坐标轴围成的四边形恰好有外接圆,则a与b的值分别为( )
A.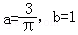 B.
B.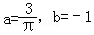
C.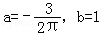 D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com