Question

8．已知△ABC的三个顶点坐标分别为A（-2，3），B（-2，-1），C（6，-1），以原点为圆心的圆与此三角形有唯一的公共点，则圆的方程为（　　）

• A． x²+y²=1
• B． x²+y²=4
• C． x²+y²=$\frac{16}{5}$
• D． x²+y²=1或x²+y²=37

Answer 1

分析 由题意画出图形，结合以原点为圆心的圆与此三角形有唯一的公共点，求出圆的半径，则圆的方程可求．

解答 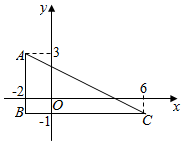解：如图
A（-2，3），C（6，-1），
∴过A、C的直线方程为$\frac{y+1}{3+1}=\frac{x-6}{-2-6}$，化为一般式方程，x+2y-4=0．
点O到直线x+2y-4=0的距离d=$\frac{|-4|}{\sqrt{5}}=\frac{4\sqrt{5}}{5}＞1$，
又OA=$\sqrt{（-2）^{2}+{3}^{2}}=\sqrt{13}$，OB=$\sqrt{（-2）^{2}+（-1）^{2}}=\sqrt{5}$，OC=$\sqrt{{6}^{2}+（-1）^{2}}=\sqrt{37}$．
∴以原点为圆心的圆若与三角形ABC有唯一的公共点，则公共点为（0，-1）或（6，-1），
∴圆的半径为1或$\sqrt{37}$，
则圆的方程为x²+y²=1或x²+y²=37．
故选：D．

点评 本题考查圆的标准方程，考查了数形结合的解题思想方法，是中档题．