
设动点P在棱长为1的正方体ABCD-A1B1C1D1的对角线BD1上,记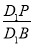 =λ.当∠APC为钝角时,λ的取值范围是________.
=λ.当∠APC为钝角时,λ的取值范围是________.
(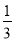 ,1)
,1)
【解析】本题主要考查了用空间向量求直线间的夹角,一元二次不等式的解法,意在考查考生的空间想象能力以及运算求解能力.
以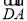 、
、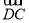 、
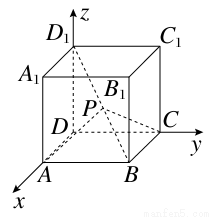
、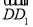 为单位正交基底,建立如图所示的空间直角坐标系D-xyz,则有A(1,0,0),B(1,1,0),C(0,1,0),D1(0,0,1),则
为单位正交基底,建立如图所示的空间直角坐标系D-xyz,则有A(1,0,0),B(1,1,0),C(0,1,0),D1(0,0,1),则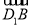 =(1,1,-1),得
=(1,1,-1),得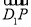 =λ
=λ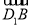 =(λ,λ,-λ),所以
=(λ,λ,-λ),所以 =
=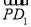 +
+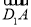 =(-λ,-λ,λ)+(1,0,-1)=(1-λ,-λ,λ-1),
=(-λ,-λ,λ)+(1,0,-1)=(1-λ,-λ,λ-1),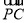 =
=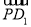 +
+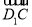 =(-λ,-λ,λ)+(0,1,-1)=(-λ,1-λ,λ-1),显然∠APC不是平角,所以∠APC为钝角等价于
=(-λ,-λ,λ)+(0,1,-1)=(-λ,1-λ,λ-1),显然∠APC不是平角,所以∠APC为钝角等价于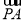 ·
·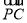 <0,即-λ(1-λ)-λ(1-λ)+(λ-1)2<0,即(λ-1)(3λ-1)<0,解得
<0,即-λ(1-λ)-λ(1-λ)+(λ-1)2<0,即(λ-1)(3λ-1)<0,解得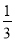 <λ<1,因此λ的取值范围是(
<λ<1,因此λ的取值范围是(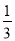 ,1).
,1).


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-5椭圆(解析版) 题型:选择题
已知椭圆C: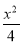 +
+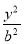 =1(b>0),直线l:y=mx+1,若对任意的m∈R,直线l与椭圆C恒有公共点,则实数b的取值范围是( )
=1(b>0),直线l:y=mx+1,若对任意的m∈R,直线l与椭圆C恒有公共点,则实数b的取值范围是( )
A.[1,4) B.[1,+∞)
C.[1,4)∪(4,+∞) D.(4,+∞)
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-2直线的交点坐标与距离公式(解析版) 题型:填空题
已知直线l1:ax-y+2a=0,l2:(2a-1)x+ay+a=0互相垂直,则实数a的值是________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-1直线的倾斜角与斜率、直线方程(解析版) 题型:填空题
已知点A(3,0),B(0,4),直线AB上一动点P(x,y),则xy的最大值是________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-7立体几何中的向量方法(解析版) 题型:选择题
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,2AC=AA1=BC=2.若二面角B1-DC-C1的大小为60°,则AD的长为( )

A. B.
B.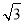 C.2 D.
C.2 D.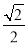
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-7立体几何中的向量方法(解析版) 题型:选择题
如图所示,ABCD-A1B1C1D1是棱长为6的正方体,E、F分别是棱AB、BC上的动点,且AE=BF.当A1、E、F、C1共面时,平面A1DE与平面C1DF所成二面角的余弦值为( )
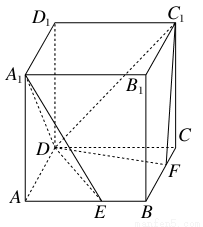
A.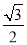 B.
B.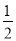 C.
C.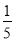 D.
D.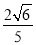
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-6空间向量及运算(解析版) 题型:解答题
如图所示,已知空间四边形ABCD的每条边和对角线长都等于1,点E、F、G分别是AB、AD、CD的中点,计算:
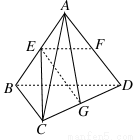
(1) ·
·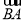 ;
;
(2) ·
·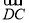 ;
;
(3)EG的长;
(4)异面直线AG与CE所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-5直线、平面垂直的判定及性质(解析版) 题型:填空题
设α、β、γ为彼此不重合的三个平面,l为直线,给出下列命题:
①若α∥β,α⊥γ,则β⊥γ;
②若α⊥γ,β⊥γ,且α∩β=l,则l⊥γ;
③若直线l与平面α内的无数条直线垂直,则直线l与平面α垂直;
④若α内存在不共线的三点到β的距离相等,则平面α平行于平面β;
上面命题中,真命题的序号为________(写出所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-2空间几何体的表面积和体积(解析版) 题型:解答题
一个多面体的直观图及三视图如图所示:(其中M、N分别是AF、BC的中点)
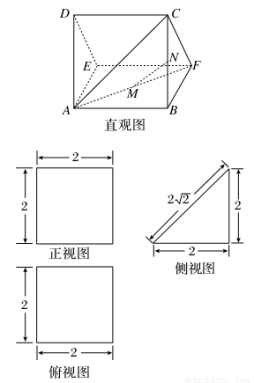
(1)求证:MN∥平面CDEF;
(2)求多面体A-CDEF的体积.
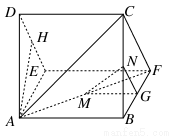
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com