
| A. | (-∞,1] | B. | (+∞,1) | C. | (+∞,2) | D. | (+∞,2) |
分析 由题意,复合函数f(x)在区间[1,+∞)上是增函数可得出内层函数t=|x-a|在区间[1,+∞)上是增函数,又绝对值函数t=|x-a|在区间[a,+∞)上是增函数,可得出[1,+∞)⊆[a,+∞),比较区间端点即可得出a的取值范围.
解答 解:因为函数f(x)=e|x-a|(a为常数).若f(x)在区间[1,+∞)上是增函数
由复合函数的单调性知,必有t=|x-a|在区间[1,+∞)上是增函数
又t=|x-a|在区间[a,+∞)上是增函数
所以[1,+∞)⊆[a,+∞),故有a≤1
故选:A.
点评 本题考查指数函数单调性的运用及复合函数单调性的判断,集合包含关系的判断,解题的关键是根据指数函数的单调性将问题转化为集合之间的包含关系,本题考查了转化的思想及推理判断的能力,属于指数函数中综合性较强的题型.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x2+2x+2≤0 | B. | 任意一个四边形的四个顶点共圆 | ||
| C. | ?x∈R,sin2x+cos2x=1 | D. | 所有能被3整除的整数都是奇数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
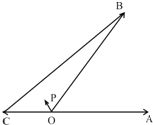 如图:已知$\overrightarrow{OC}=-\frac{1}{2}\overrightarrow{OA}$,若$\overrightarrow{OP}$的终点P在△OBC的边界及内部,且$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$则x、y满足的条件为( )
如图:已知$\overrightarrow{OC}=-\frac{1}{2}\overrightarrow{OA}$,若$\overrightarrow{OP}$的终点P在△OBC的边界及内部,且$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$则x、y满足的条件为( )| A. | $\left\{{\begin{array}{l}{-\frac{1}{2}≤x≤0}\\{0≤y≤1}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{x≤0}\\{y≥0}\\{y-2x-1≤0}\end{array}}\right.$ | ||
| C. | $\left\{{\begin{array}{l}{x≤0}\\{y≥0}\\{2y-x-1≤0}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{-\frac{1}{2}≤x≤0}\\{0≤y≤1}\\{y-2x-1≤0}\end{array}}\right.$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | -4 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①②③ | D. | ①②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 50 | B. | 25 | C. | 100 | D. | $2\sqrt{20}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}sin2θ$ | B. | $-\frac{1}{2}sin2θ$ | C. | sin2θ | D. | -sin2θ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com