
分析 取高线的$\frac{1}{3}$点,过该点作平行于底的平面,若VQ-ABC<$\frac{1}{3}{V_{P-ABC}}$,则Q点在平面DEF与底面ABC之间,所以概率为棱台与原棱锥体积之比,用相似比计算即可.
解答 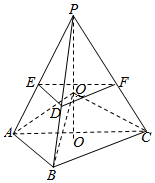 解:作出P在底面△ABC的射影为O
解:作出P在底面△ABC的射影为O
若VQ-ABC=$\frac{1}{3}$VP-ABC,则高OQ=$\frac{1}{3}$PO,
则VQ-ABC<$\frac{1}{3}{V_{P-ABC}}$的点Q位于在三棱锥VP-ABC的截面DEF以下的棱台内,
则对应的概率P=1-($\frac{2}{3}$)3=$\frac{19}{27}$,
故答案为:$\frac{19}{27}$.
点评 本题主要考查几何概型的概率计算,求出对应的体积关系是解决本题的关键,根据比例关系,得到面积之比是相似比的平方,体积之比是相似比的立方.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 4 | C. | 8 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
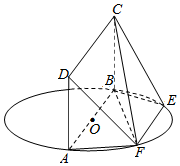 如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD所在平面和圆O所在的平面互相垂直.已知AB=2,EF=1.
如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD所在平面和圆O所在的平面互相垂直.已知AB=2,EF=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com