
分析 (Ⅰ)f(x+1)+f(x+3)=|x-1|+|x+1|,而|x-1|+|x+1|≥|(x-1)-(x+1)|=2,当且仅当|(x-1)(x+1)≤0,即-1≤x≤1时取等号.即可得出结论;
(Ⅱ)利用作差法进行证明即可.
解答 (Ⅰ)解:f(x+1)+f(x+3)=|x-1|+|x+1|,而|x-1|+|x+1|≥|(x-1)-(x+1)|=2,
当且仅当|(x-1)(x+1)≤0,即-1≤x≤1时取等号.
因此M={x|x<-1或x>1}. …(5分)
(Ⅱ)证明:$f(ab)<|a|•f(\frac{b}{a})?|ab-2|<|b-2a|$,
因为a∈M,|b|<2,所以(ab-2)2-(b-2a)2=a2b2-4a2-b2+4=(a2-1)(b2-4)<0.
因此|b-a|<|b-2a|,故$f(ab)<|a|•f(\frac{b}{a})$.…(10分)
点评 本题考查绝对值不等式的解法,考查不等式的证明,考查学生分析解决问题的能力,属于中档题.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:选择题
| A. | 1或3 | B. | 1 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
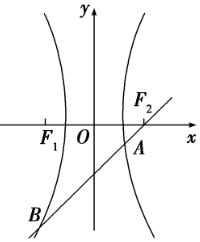 过双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1的右焦点作倾斜角为45°的弦AB.求:
过双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1的右焦点作倾斜角为45°的弦AB.求:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | .6 | B. | 8 | C. | 10 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -144 | B. | -136 | C. | -57 | D. | 34 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com