
【题目】在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]() :
:![]() ,过抛物线焦点
,过抛物线焦点![]() 且与
且与![]() 轴垂直的直线与抛物线相交于
轴垂直的直线与抛物线相交于![]() 、
、![]() 两点,且
两点,且![]() 的周长为
的周长为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)若直线![]() 过焦点
过焦点![]() 且与抛物线
且与抛物线![]() 相交于
相交于![]() 、
、![]() 两点,过点
两点,过点![]() 、
、![]() 分别作抛物线
分别作抛物线![]() 的切线
的切线![]() 、
、![]() ,切线
,切线![]() 与
与![]() 相交于点
相交于点![]() ,求:
,求:![]() 的值.
的值.
【答案】(1)![]() ;(2)0.
;(2)0.
【解析】
(1)先求得A,B两点坐标,利用计算![]() 的周长可得p,进而求得抛物线方程;
的周长可得p,进而求得抛物线方程;
(2)利用导数的几何意义求得切线![]() 与
与![]() 的方程,联立直线与抛物线方程,利用韦达定理及
的方程,联立直线与抛物线方程,利用韦达定理及![]() 与
与![]() 的交点P,可得
的交点P,可得![]() ,再利用焦半径公式求得
,再利用焦半径公式求得![]() ,可得结果.
,可得结果.
(1)由题意知焦点![]() 的坐标为
的坐标为![]() ,将
,将![]() 代入抛物线
代入抛物线![]() 的方程可求得点
的方程可求得点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ,
,
有![]() ,
,![]() ,可得
,可得![]() 的周长为
的周长为![]() ,有
,有![]() ,得
,得![]() .
.
故抛物线![]() 的方程为
的方程为![]() .
.
(2)由(1)知抛物线![]() 的方程可化为
的方程可化为![]() ,求导可得
,求导可得![]() .
.
设点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、![]() .
.
设直线![]() 的方程为
的方程为![]() (直线
(直线![]() 的斜率显然存在).
的斜率显然存在).
联立方程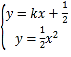 消去
消去![]() 整理为:
整理为:![]() ,可得
,可得![]() .
.
有![]() ,
,![]() .
.
可得直线![]() 的方程为
的方程为![]() ,整理为
,整理为![]() .
.
同理直线![]() 的方程为
的方程为![]() .
.
联立方程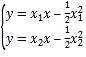 ,解得
,解得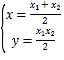 ,则点
,则点![]() 的坐标为
的坐标为![]() .
.
由抛物线的几何性质知![]() ,
,![]() ,
,
![]() .
.
有![]()
![]() .
.
∴![]() .
.


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案科目:高中数学 来源: 题型:
【题目】为响应“文化强国建设”号召,并增加学生们对古典文学的学习兴趣,雅礼中学计划建设一个古典文学熏陶室.为了解学生阅读需求,随机抽取200名学生做统计调查.统计显示,男生喜欢阅读古典文学的有64人,不喜欢的有56人;女生喜欢阅读古典文学的有36人,不喜欢的有44人.
(1)能否在犯错误的概率不超过0.25的前提下认为喜欢阅读古典文学与性别有关系?
(2)为引导学生积极参与阅读古典文学书籍,语文教研组计划牵头举办雅礼教育集团古典文学阅读交流会.经过综合考虑与对比,语文教研组已经从这200人中筛选出了5名男生代表和4名女生代表,其中有3名男生代表和2名女生代表喜欢古典文学.现从这9名代表中任选3名男生代表和2名女生代表参加交流会,记![]() 为参加交流会的5人中喜欢古典文学的人数,求
为参加交流会的5人中喜欢古典文学的人数,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
附: ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,其焦距为
,其焦距为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,
上,![]() ,直线
,直线![]() 的斜率为
的斜率为![]() (
(![]() 为半焦距)·
为半焦距)·
(1)求椭圆![]() 的方程;
的方程;
(2)设圆![]() 的切线
的切线![]() 交椭圆
交椭圆![]() 于
于![]() 两点(
两点(![]() 为坐标原点),求证:
为坐标原点),求证:![]() ;
;
(3)在(2)的条件下,求![]() 的最大值
的最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某圆柱的高为2,底面周长为16,其三视图如图所示,圆柱表面上的点![]() 在正视图上的对应点为
在正视图上的对应点为![]() ,圆柱表面上的点
,圆柱表面上的点![]() 在左视图上的对应点为
在左视图上的对应点为![]() ,则在此圆柱侧面上,从
,则在此圆柱侧面上,从![]() 到
到![]() 的路径中,最短路径的长度为( )
的路径中,最短路径的长度为( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4一4:坐标系与参数方程
在平面直角坐标系xOy中,曲线![]() 的参数方程为
的参数方程为![]() 参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线
参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线![]() 是圆心的极坐标为(
是圆心的极坐标为(![]() )且经过极点的圆
)且经过极点的圆
(1)求曲线C1的极坐标方程和C2的普通方程;
(2)已知射线![]() 分別与曲线C1,C2交于点A,B(点B异于坐标原点O),求线段AB的长
分別与曲线C1,C2交于点A,B(点B异于坐标原点O),求线段AB的长
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,过曲线![]() 外的一点
外的一点![]() (其中
(其中![]() ,
,![]() 为锐角)作平行于
为锐角)作平行于![]() 的直线
的直线![]() 与曲线分别交于
与曲线分别交于![]() .
.
(Ⅰ) 写出曲线![]() 和直线
和直线![]() 的普通方程(以极点为原点,极轴为
的普通方程(以极点为原点,极轴为![]() 轴的正半轴建系);
轴的正半轴建系);
(Ⅱ)若![]() 成等比数列,求
成等比数列,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年4月10日21时整,全球六地(上海和台北、布鲁塞尔、圣地亚哥、东京和华盛顿同时召开新闻发布会,宣布人类首次利用虚拟射电望远镜,成功捕获世界上首张黑洞图像,公布的照片展示了一个中心为黑色的明亮环状结构,看上去有点像个橙色的甜甜圈,其黑色部分是黑洞投下的“阴影”,明亮部分是绕黑洞高速旋转的吸积盘.某同学作了一张黑洞示意图,如图所示,由两个同心圆和半个同心圆环构成圆及圆环的半径从内到外依次为2,3,4,5个单位在图中随机任取一点,则该点取自阴影的概率为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆锥的顶点为A,高和底面的半径相等,BE是底面圆的一条直径,点D为底面圆周上的一点,且∠ABD=60°,则异面直线AB与DE所成角的正弦值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com