
分析 (Ⅰ)由条件可得正方形的边长为$\sqrt{2}$,对角线长为2,即有m=c=1,分别将P的坐标代入双曲线的方程和椭圆方程,即可得到所求椭圆和双曲线的方程;
(Ⅱ)假设存在直线l:y=kx+t,使得此直线l与椭圆Г相切、与双曲线S相交于A,B两点,且满足|$\overrightarrow{AB}$|=|$\overrightarrow{OA}$$+\overrightarrow{OB}$|.将直线方程代入椭圆方程,运用判别式为0,可得3k2=t2-2,再将直线方程代入双曲线的方程,运用韦达定理和判别式大于0,由向量的加减运算和数量积的坐标表示,解方程可得t,即可判断不存在.
解答 解:(Ⅰ)四边形F1G1F2G2为正方形,且这个正方形的面积为2,
可得正方形的边长为$\sqrt{2}$,对角线长为2,
即有m=c=1,
P(1,$\frac{2\sqrt{3}}{3}$)代入双曲线的方程,可得$\frac{4}{3}$-$\frac{1}{{n}^{2}}$=1,
可得n2=3,双曲线S:y2-$\frac{{x}^{2}}{3}$=1;
P(1,$\frac{2\sqrt{3}}{3}$)代入椭圆的方程,可得$\frac{1}{{a}^{2}}$-$\frac{4}{3{b}^{2}}$=1,
又a2-b2=1,
解得a2=3,b2=2,可得椭圆的方程为$\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{2}$=1;
(Ⅱ)假设存在直线l:y=kx+t,使得此直线l与椭圆Г相切、
与双曲线S相交于A,B两点,且满足|$\overrightarrow{AB}$|=|$\overrightarrow{OA}$$+\overrightarrow{OB}$|.
将直线y=kx+t代入椭圆方程,可得(2+3k2)x2+6ktx+3t2-6=0,
由△=36k2t2-4(2+3k2)(3t2-6)=0,
可得3k2=t2-2,
由y=kx+t代入双曲线的方程,可得(3k2-1)x2+6ktx+3t2-3=0,
设A(x1,y1),B(x2,y2),
即有x1+x2=-$\frac{6kt}{3{k}^{2}-1}$,x1x2=$\frac{3{t}^{2}-3}{3{k}^{2}-1}$,
判别式为36k2t2-4(2k2-1)(3t2-3)>0,化为t2+3k2-1>0,
即有2t2>3.
由|$\overrightarrow{AB}$|=|$\overrightarrow{OA}$$+\overrightarrow{OB}$|,可得|$\overrightarrow{OB}$-$\overrightarrow{OA}$|=|$\overrightarrow{OA}$$+\overrightarrow{OB}$|.
两边平方可得$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,
即有x1x2+y1y2=0,即为x1x2+(kx1+t)(kx2+t)=0,
即有(1+k2)x1x2+kt(x1+x2)+t2=0,
即为(1+k2)($\frac{3{t}^{2}-3}{3{k}^{2}-1}$)+t2+kt(-$\frac{6kt}{3{k}^{2}-1}$)=0,
化简为2t2-3-3k2=0,
解得t2=1,与2t2>3.矛盾,
可得不存在直线l:y=kx+t.
点评 本题考查椭圆和双曲线的方程的求法,注意运用点满足方程,考查直线和椭圆相切的条件:判别式为0,直线和双曲线的方程联立,运用韦达定理和判别式大于0,同时考查向量的数量积的坐标表示,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
 如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横、纵坐标分别对应数列{an}(n∈N*)的前12项(即横坐标为奇数项,纵坐标为偶数项),按如此规律下去.a2016等于( )
如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横、纵坐标分别对应数列{an}(n∈N*)的前12项(即横坐标为奇数项,纵坐标为偶数项),按如此规律下去.a2016等于( )| A. | 1007 | B. | 1008 | C. | -1008 | D. | 2016 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
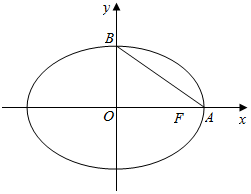 已知椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1(0<b<2),设点A(2,0),B(0,b)与直线AB斜率相同的直线与椭圆交于M,N两点,设MN中点的轨迹为C.
已知椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1(0<b<2),设点A(2,0),B(0,b)与直线AB斜率相同的直线与椭圆交于M,N两点,设MN中点的轨迹为C.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | -1 | C. | 0 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com