
分析 作出草图:先根据题意确定PA、PB、PC和BC的值,在△BPC中应用余弦定理可求得cos2θ的值,进而可确定2θ的值,然后在△PCD中可求得PD的长度,从而确定答案.
解答 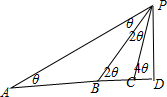 解:如图,依题意有PB=BA=3,PC=BC=$\sqrt{3}$.
解:如图,依题意有PB=BA=3,PC=BC=$\sqrt{3}$.
在△BPC中,由余弦定理可得
cos2θ=$\frac{(\sqrt{3})^{2}+{3}^{2}-(\sqrt{3})^{2}}{2×\sqrt{3}×3}$=$\frac{\sqrt{3}}{2}$,
所以2θ=30°,4θ=60°,θ=15°
在△PCD中,
可得PD=PC•sin4θ=$\sqrt{3}$•$\frac{\sqrt{3}}{2}$=$\frac{3}{2}$(千米).
点评 本题主要考查余弦定理的应用.考查应用余弦定理解决实际问题的能力.


 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:解答题
 如图正四棱锥S-ABCD,底面边长为2,P为侧棱SD上靠近D的三等分点,
如图正四棱锥S-ABCD,底面边长为2,P为侧棱SD上靠近D的三等分点,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则y=f(x)的图象可由y=cos2x图象( )
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则y=f(x)的图象可由y=cos2x图象( )| A. | 向右平移$\frac{π}{3}$个长度单位 | B. | 向左平移$\frac{π}{3}$个长度单位 | ||
| C. | 向右平移$\frac{π}{6}$个长度单位 | D. | 向左平移$\frac{π}{6}$个长度单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知四棱锥P-ABCD,AD∥BC,AB⊥BC,AD=2,AB=BC=PC=PD=1,∠APD=90°.
已知四棱锥P-ABCD,AD∥BC,AB⊥BC,AD=2,AB=BC=PC=PD=1,∠APD=90°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
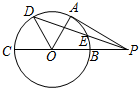 如图,PA切圆O于点A,割线PBC经过圆心O,若PB=OB=1,OD平分∠AOC,交圆O于点D,连接PD交圆O于点E,则PE的长等于( )
如图,PA切圆O于点A,割线PBC经过圆心O,若PB=OB=1,OD平分∠AOC,交圆O于点D,连接PD交圆O于点E,则PE的长等于( )| A. | $\frac{{\sqrt{7}}}{7}$ | B. | $\frac{{3\sqrt{7}}}{7}$ | C. | $\frac{{5\sqrt{7}}}{7}$ | D. | $\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD中,AB,AD,AP两两垂直,长度分别为1,2,2,且$\overrightarrow{DC}$=2$\overrightarrow{AB}$.
如图,四棱锥P-ABCD中,AB,AD,AP两两垂直,长度分别为1,2,2,且$\overrightarrow{DC}$=2$\overrightarrow{AB}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>1 | B. | a>1或a=-3 | C. | 0<a<1或a=-3 | D. | a>-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com