
| A�� | 3�� | B�� | $\sqrt{3}$�� | C�� | 3$\sqrt{3}$�� | D�� | $\sqrt{6}$�� |
���� ���ȣ�����������ʽ��Ȼ���ͼ�Σ�ȷ���û����Ե�Բ�ĽǼ��ɣ�
���  �⣺����Բ$\left\{\begin{array}{l}{x=3+3\sqrt{3}cos��}\\{y=3\sqrt{3}sin��}\end{array}\right.$����Ϊ������
�⣺����Բ$\left\{\begin{array}{l}{x=3+3\sqrt{3}cos��}\\{y=3\sqrt{3}sin��}\end{array}\right.$����Ϊ������
�ã�x-3��2+y2=27��Բ��Ϊ��3��0�����뾶Ϊ3$\sqrt{3}$��
��Բ$\left\{\begin{array}{l}{x=3cos��}\\{y=3sin��}\end{array}\right.$��
��x2+y2=9��Բ��Ϊ��0��0�����뾶Ϊ3��
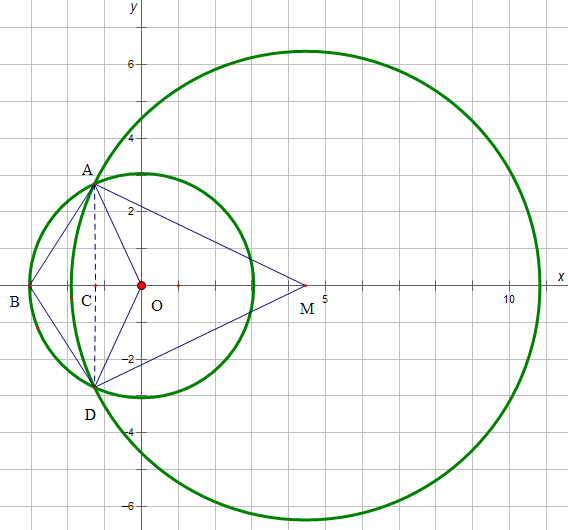
��ͼ��ʾ������A��x��Ĵ��ߣ�����Ϊ��C�����ڡ�ABO�У���������Ϊ�ȱ������Σ�
�õ�AC=$\frac{3\sqrt{3}}{2}$����ֱ��������ACM�У���AMC=30�㣬
��$\widehat{ABD}$=$\frac{��}{3}��3\sqrt{3}$=$\sqrt{3}��$��
��ѡB��
���� �����ص㿼����Բ�IJ������̺���ͨ���̵Ļ�����������ʽ��֪ʶ�������е��⣮


 ����С����ͬ������ϵ�д�
����С����ͬ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{3}$a+$\frac{2}{3}$b | B�� | $\frac{2}{3}$a+$\frac{1}{3}$b | C�� | $\frac{1}{3}a$-$\frac{2}{3}$b | D�� | $\frac{2}{3}$a-$\frac{1}{3}$b |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-2��+�ޣ� | B�� | ��-2��$\sqrt{2}+1$�� | C�� | ��-�ޣ�$\sqrt{2}+1$�� | D�� | ��-$\sqrt{2}+1$��$\sqrt{2}+1$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com