
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的离心率为
的离心率为![]() ,右顶点为
,右顶点为![]() ,直线
,直线![]() 过原点
过原点![]() ,且点
,且点![]() 在x轴的上方,直线
在x轴的上方,直线![]() 与
与![]() 分别交直线
分别交直线![]() :
: ![]() 于点
于点![]() 、
、![]() .
.
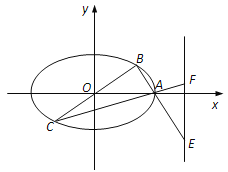
(1)若点![]() ,求椭圆的方程及△ABC的面积;
,求椭圆的方程及△ABC的面积;
(2)若![]() 为动点,设直线
为动点,设直线![]() 与
与![]() 的斜率分别为
的斜率分别为![]() 、
、![]() .
.
①试问![]() 是否为定值?若为定值,请求出;否则,请说明理由;
是否为定值?若为定值,请求出;否则,请说明理由;
②求△AEF的面积的最小值.
【答案】(1)![]()
![]() (2)①
(2)①![]() ②
②![]()
【解析】试题分析:(1)根据题意的离心率及点B的坐标,建立方程,求出a的值,即可求△ABC的面积;(2)①![]() 为定值,证明
为定值,证明![]() ,由(1)得
,由(1)得![]() ,即可得到结论;②设直线AB的方程为y=k1(x-a),直线AC的方程为y=k2(x-a),令x=a+1得,求出△AEF的面积,结合①的结论,利用基本不等式,可求△AEF的面积的最小值
,即可得到结论;②设直线AB的方程为y=k1(x-a),直线AC的方程为y=k2(x-a),令x=a+1得,求出△AEF的面积,结合①的结论,利用基本不等式,可求△AEF的面积的最小值
试题解析:(1)由题意得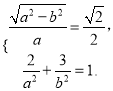 解得
解得![]()
椭圆的方程为![]() ……………………………………………………3分
……………………………………………………3分
△ABC的面积![]() .………………………4分
.………………………4分
(2)①![]() 为定值,下证之:
为定值,下证之:
证明:设![]() ,则
,则![]() ,且
,且![]() .………………5分
.………………5分
而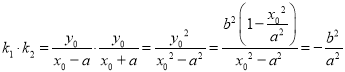 ………………………7分
………………………7分
由离心率![]() ,得
,得![]()
所以![]() ,为定值.……………………………………………8分
,为定值.……………………………………………8分
②由直线的点斜式方程,得直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 的方程为
的方程为![]() . 令
. 令
![]() ,得
,得![]() ,
, ![]() .
.
所以,△AEF的面积![]() …………………………10分
…………………………10分
由题意,直线![]() 的斜率
的斜率![]() . 由①,
. 由①, ![]()
于是, 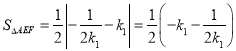
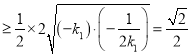 ,
,
当且仅当![]() ,即
,即![]() 时取等号.………………………………11分
时取等号.………………………………11分
所以,△AEF的面积的最小值为![]() .………12分
.………12分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】为贯彻落实教育部等6部门《关于加快发展青少年校园足球的实施意见》,全面提高我市中学生的体质健康水平,普及足球知识和技能,市教体局决定矩形春季校园足球联赛,为迎接此次联赛,甲同学选拔了20名学生组成集训队,现统计了这20名学生的身高,记录如下表:
身高( | 168 | 174 | 175 | 176 | 178 | 182 | 185 | 188 |
人数 | 1 | 2 | 4 | 3 | 5 | 1 | 3 | 1 |
(1)请计算这20名学生的身高中位数、众数,并补充完成下面的茎叶图;

(2)身高为185![]() 和188
和188![]() 的四名学生分别为
的四名学生分别为![]() ,
,![]() ,
,![]() ,
,![]() ,先从这四名学生中选2名担任正副门将,请利用列举法列出所有可能情况,并求学生
,先从这四名学生中选2名担任正副门将,请利用列举法列出所有可能情况,并求学生![]() 入选正门将的概率.
入选正门将的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先后2次抛掷一枚骰子,将得到的点数分别记为![]() .
.
(Ⅰ)求满足![]() 的概率;
的概率;
(Ⅱ)设三条线段的长分别为![]() 和5,求这三条线段能围成等腰三角形(含等边三角形)的概率.
和5,求这三条线段能围成等腰三角形(含等边三角形)的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,cos C=.
(1)若·=,求c的最小值;
(2)设向量x=(2sin B,-),y=,且x∥y,求sin(B-A)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的右顶点到其一条渐近线的距离等于
的右顶点到其一条渐近线的距离等于![]() ,抛物线
,抛物线![]() 的焦点与双曲线
的焦点与双曲线![]() 的右焦点重合,则抛物线
的右焦点重合,则抛物线![]() 上的动点
上的动点![]() 到直线
到直线![]() 和
和![]() 的距离之和的最小值为__________.
的距离之和的最小值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为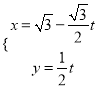 (
(![]() 为参数),以原点为极点,
为参数),以原点为极点, ![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,与曲线
,与曲线![]() 的交点为
的交点为![]() ,
, ![]() ,若
,若![]() 的中点为
的中点为![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, 椭圆![]() 的离心率是
的离心率是![]() ,点
,点![]() 在椭圆上, 设点
在椭圆上, 设点![]() 分别是椭圆的右顶点和上顶点, 过 点
分别是椭圆的右顶点和上顶点, 过 点![]() 引椭圆
引椭圆![]() 的两条弦
的两条弦![]() 、
、![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与
与![]() 的斜率是互为相反数.
的斜率是互为相反数.
①直线![]() 的斜率是否为定值?若是求出该定值, 若不是,说明理由;
的斜率是否为定值?若是求出该定值, 若不是,说明理由;
②设![]() 、
、![]() 的面积分别为
的面积分别为![]() 和
和![]() ,求
,求![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天气预报显示,在今后的三天中,每一天下雨的概率为40%,现用随机模拟的方法估计这三天中恰有两天下雨的概率:先利用计算器产生0--9之间整数值的随机数,并制定用1,2,3,4表示下雨,用5,6,7,8,9,0表示不下雨,再以每3个随机数作为一组,代表三天的天气情况,产生了如下20组随机数
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
则这三天中恰有两天下雨的概率近似为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校随机抽取部分新生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学路上所需时间的范围是![]() ,样本数据分组为
,样本数据分组为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
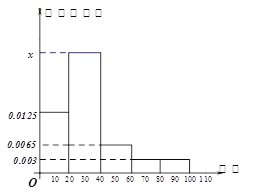
(1)求直方图中![]() 的值;
的值;
(2)如果上学路上所需时间不少于40分钟的学生可申请在学校住宿,请估计学校1000名新生中有多少名学生可以申请住宿.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com