
分析 (1)利用公式${a}_{n}=\left\{\begin{array}{l}{{S}_{1},n=1}\\{{S}_{n}-{S}_{n-1},n≥2}\end{array}\right.$得出{an}为等比数列,代入bn=log2an得出{bn}的通项公式;
(2)求出cn,使用裂项求和得出Tn,代入不等式得出k≥$\frac{2n-9}{{2}^{n}}$,求出判定数列{$\frac{2n-9}{{2}^{n}}$}的增减性得出最大项,从而得出k的最小值.
解答 解:(1)∵3Sn=4an-4
∴n=1时,3a1=4a1-4,∴a1=4.
当n≥2时,3Sn-1=4an-1-4,∴3an=3Sn-3Sn-1=4an-4an-1,即$\frac{a_n}{{{a_{n-1}}}}=4$,
∴{an} 是一个首项为4,公比为4的等比数列,∴${a_n}={4^n}$,
∴bn=log2an=log24n=2n.
(2)cn=b1+b2+…+bn=$\frac{2+2n}{2}•n$=n(n+1).
∴Tn=$\frac{1}{1×2}+\frac{1}{2×3}+$…+$\frac{1}{n(n+1)}$=1-$\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+$…+$\frac{1}{n}-\frac{1}{n+1}$=$\frac{n}{n+1}$.
∵$k•\frac{{n•{2^n}}}{n+1}≥(2n-9){T_n}$=$\frac{(2n-9)•n}{n+1}$恒成立,
∴k≥$\frac{2n-9}{{2}^{n}}$恒成立.
设dn=$\frac{2n-9}{{2}^{n}}$,则dn+1-dn=$\frac{2n-7}{{2}^{n+1}}$-$\frac{2n-9}{{2}^{n}}$=$\frac{11-2n}{{2}^{n+1}}$,
∴当n≥6时,数列{dn}单调递减,当1≤n≤5时,数列{dn}单调递增;
∴数列{dn}最大项为d6=$\frac{3}{64}$,
∴k≥$\frac{3}{64}$.
点评 本题考查了数列通项公式的求法,数列求和及数列单调性的应用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 10份 | B. | 20份 | C. | 30份 | D. | 40份 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2k-1 | B. | 2k-1 | C. | 2k | D. | 2k+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
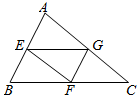 如图,在△ABC中,AB=2$\sqrt{5}$,BC=2$\sqrt{10}$,AC=2$\sqrt{13}$,E、F、G分别为三边中点,将△BEF,△AEG,△GCF分别沿EF、EG、GF向上折起,使A、B、C重合,记为S,则三棱锥S-EFG的外接球面积为( )
如图,在△ABC中,AB=2$\sqrt{5}$,BC=2$\sqrt{10}$,AC=2$\sqrt{13}$,E、F、G分别为三边中点,将△BEF,△AEG,△GCF分别沿EF、EG、GF向上折起,使A、B、C重合,记为S,则三棱锥S-EFG的外接球面积为( )| A. | 14π | B. | 15π | C. | $\frac{29}{2}$π | D. | 2$\sqrt{33}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m>n | B. | m<n | C. | m=n | D. | m≤n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com