
���� �������Ľ���ʽ�������������ֵ�жϢٵ������������Ǻ�����ͼ���ƽ���жϢڵ�������������ĵ����������жϢ۵�������������ĶԳ������жϢܵ�����
��� �⣺���ڢ٣���Ϊf��x��=2sinxcosx-2cos2x=$\sqrt{2}$sin��2x-$\frac{��}{4}$��-1���������ֵΪ$\sqrt{2}$-1���ʢٴ���
���ڢڣ���f��x��=$\sqrt{2}$sin2x-1��ͼ������ƽ��$\frac{��}{4}$����λ��õ�f��x��=$\sqrt{2}$sin��2x-$\frac{��}{2}$��-1��ͼ������f��x��=2��sinx-cosx��cosx=sin2x-cos2x-1=$\sqrt{2}$sin��2x-$\frac{��}{4}$��-1��
�ʢڴ���
���ڢۣ���-$\frac{��}{2}$+2k�С�2x-$\frac{��}{4}$��$\frac{��}{2}$+2k�У���-$\frac{��}{8}$+k�С�x��$\frac{3��}{8}$+k�У�k��Z����������Ϊ[k��+$\frac{7��}{8}$��k��+$\frac{11��}{8}$��k��Z�����ʢ���ȷ��
���ڢܣ���2x-$\frac{��}{4}$=k�У�k��Z����x=$\frac{k��}{2}$+$\frac{��}{8}$��k��Z�����Ժ����ĶԳ�����Ϊ��$\frac{k}{2}$��+$\frac{��}{8}$��-1����k��Z�����ʢ���ȷ��
�ʴ�Ϊ���ۢܣ�
���� ���⿼�����Ǻ����Ļ�����ֵ�������ĵ������Լ�������ͼ���ƽ�ƣ����Ǻ����ĶԳ����ģ����е��⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
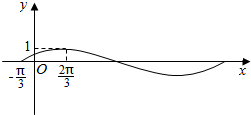
| A�� | $��=1����=\frac{��}{3}$ | B�� | $��=1����=-\frac{��}{3}$ | C�� | $��=\frac{1}{2}����=\frac{��}{6}$ | D�� | $��=\frac{1}{2}����=-\frac{��}{6}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��2 | B�� | a��3 | C�� | a��3 | D�� | a��3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��һ�鳤Ϊ8�ף���Ϊ5�ij����θְ壮
��һ�鳤Ϊ8�ף���Ϊ5�ij����θְ壮�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com