
分析 联立$\left\{\begin{array}{l}{y=kx-1}\\{x+y-1=0}\end{array}\right.$,k≠-1,解得交点.根据直线l1:y=kx-1与直线l2:x+y-1=0的交点位于第一象限,即可得出.
解答 解:联立$\left\{\begin{array}{l}{y=kx-1}\\{x+y-1=0}\end{array}\right.$,k≠-1,
解得y=$\frac{k-1}{1+k}$,x=$\frac{2}{1+k}$.
∵直线l1:y=kx-1与直线l2:x+y-1=0的交点位于第一象限,
∴$\frac{k-1}{1+k}$>0,$\frac{2}{1+k}$>0.
解得:k>1.
则k的范围为(1,+∞).
故答案为:(1,+∞).
点评 本题考查了直线的交点、不等式的解法,考查了推理能力与计算能力,属于基础题.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:高中数学 来源: 题型:解答题
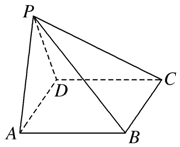 如图,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,$AB=\sqrt{3}$,BC=1,PA=2,E为PD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,$AB=\sqrt{3}$,BC=1,PA=2,E为PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [15°,45°] | B. | [15°,75°] | C. | [30°,60°] | D. | [0°,90°] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
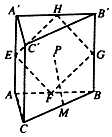 如图直三棱柱ABC-A'B'C'中,△ABC为边长为2的等边三角形,AA'=4,点E、F、G、H、M分别是边AA'、AB、BB'、A'B'、BC的中点,动点P在四边形EFGH内部运动,并且始终有MP∥平面ACC'A',则动点P的轨迹长度为( )
如图直三棱柱ABC-A'B'C'中,△ABC为边长为2的等边三角形,AA'=4,点E、F、G、H、M分别是边AA'、AB、BB'、A'B'、BC的中点,动点P在四边形EFGH内部运动,并且始终有MP∥平面ACC'A',则动点P的轨迹长度为( )| A. | 2 | B. | 2π | C. | $2\sqrt{3}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3+\sqrt{3}}{4}$a2 | B. | $\frac{3}{4}$a2 | C. | $\frac{3+\sqrt{3}}{2}$a2 | D. | $\frac{6+\sqrt{3}}{4}$a2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2),4 | B. | (1,-2),2 | C. | (-1,2),2 | D. | (1,-2),4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈(-∞,0),x3+x<0 | B. | ?x∈(-∞,0),x3+x≥0 | ||
| C. | $?{x_0}∈[0,\;+∞),\;x_0^3+{x_0}<0$ | D. | $?{x_0}∈[0,\;+∞),\;x_0^3+{x_0}≥0$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com