
分析 由题意求得n=10,在通项公式Tr+1=${C}_{10}^{r}$•(-1)r•${a}^{\frac{11r-30}{12}}$ 中,令x的幂指数等于3,求得r的值,可得展开式中含a3的项.
解答 解:由已知($\root{4}{\frac{1}{a}}-\root{3}{{a}^{2}}$)n的展开式中,倒数第3项的系数的绝对值是${C}_{n}^{n-2}$=${C}_{n}^{2}$=45,故n=10.
在通项公式Tr+1=${C}_{10}^{r}$•(-1)r•${a}^{\frac{11r-30}{12}}$ 中,令$\frac{11r-30}{12}$=3,求得r=6,
故展开式中含a3的项为 ${C}_{10}^{6}$•a3=210a3.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,二项式系数的性质,属于基础题.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中数学 来源: 题型:选择题
| A. | ac<bc | B. | $\frac{1}{a}$>$\frac{1}{b}$ | C. | $\frac{1}{a-b}$$>\frac{1}{a}$ | D. | a2<b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4a2 | B. | 4b2 | C. | 3a2+b2 | D. | a2+3b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
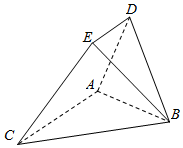 如图,以BC为斜边的等腰直角三角形ABC与等边三角形ABD所在平面互相垂直,且点E满足$\overrightarrow{DE}$=$\frac{1}{2}$$\overrightarrow{AC}$.
如图,以BC为斜边的等腰直角三角形ABC与等边三角形ABD所在平面互相垂直,且点E满足$\overrightarrow{DE}$=$\frac{1}{2}$$\overrightarrow{AC}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
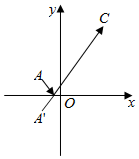 已知圆C:(x-5)2+(y-7)2=4,一束光线从点A(-1,1)经x轴反射到圆周上,求光线的最短路程,并求此时的反射光线和入射光线的方程.
已知圆C:(x-5)2+(y-7)2=4,一束光线从点A(-1,1)经x轴反射到圆周上,求光线的最短路程,并求此时的反射光线和入射光线的方程.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com