
如图,在平面直角坐标系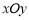 中,已知椭圆
中,已知椭圆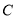 :
: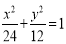 ,设
,设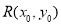 是椭圆
是椭圆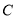 上的任一点,从原点
上的任一点,从原点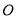 向圆
向圆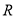 :
: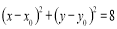 作两条切线,分别交椭圆于点
作两条切线,分别交椭圆于点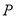 ,
,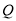 .
.

(1)若直线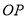 ,
,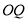 互相垂直,求圆
互相垂直,求圆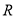 的方程;
的方程;
(2)若直线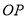 ,
,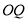 的斜率存在,并记为
的斜率存在,并记为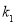 ,
,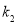 ,求证:
,求证: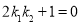 ;
;
(3)试问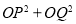 是否为定值?若是,求出该值;若不是,说明理由.
是否为定值?若是,求出该值;若不是,说明理由.
(1)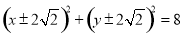 ;(2)
;(2)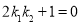 ;(3)定值为36.
;(3)定值为36.
【解析】
试题分析:(1)因为直线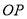 ,
,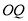 互相垂直,且和圆
互相垂直,且和圆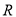 相切,所以
相切,所以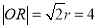 ;再结合点
;再结合点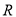 在椭圆
在椭圆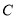 上,得到关于
上,得到关于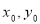 的方程组进行求解;(2)设出
的方程组进行求解;(2)设出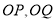 的直线方程,利用直线与圆相切,得到
的直线方程,利用直线与圆相切,得到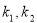 与
与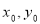 的关系;再根据
的关系;再根据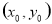 在椭圆上,得出关系,整理即可;(3)分别联立两直线与椭圆的方程,得出
在椭圆上,得出关系,整理即可;(3)分别联立两直线与椭圆的方程,得出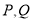 的关系,借助
的关系,借助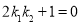 进行证明.
进行证明.
试题解析:(1)由圆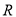 的方程知,圆
的方程知,圆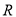 的半径的半径
的半径的半径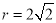 ,
,
因为直线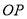 ,
,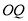 互相垂直,且和圆
互相垂直,且和圆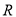 相切,
相切,
所以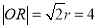 ,即
,即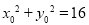 ,①
,①
又点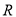 在椭圆
在椭圆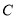 上,所以
上,所以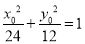 ,②
,②
联立①②,解得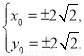
所以所求圆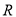 的方程为
的方程为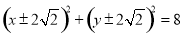 .
.
(2)因为直线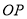 :
: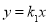 ,
,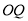 :
: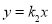 ,与圆
,与圆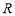 相切,
相切,
所以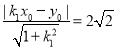 ,化简得
,化简得
同理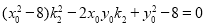 ,
,
所以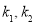 是方程
是方程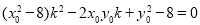 的两个不相等的实数根,
的两个不相等的实数根,
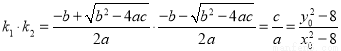
因为点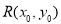 在椭圆C上,所以
在椭圆C上,所以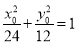 ,即
,即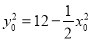 ,
,
所以 ,即
,即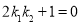 .
.
(3)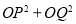 是定值,定值为36,
是定值,定值为36,
理由如下:
法一:(i)当直线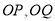 不落在坐标轴上时,设
不落在坐标轴上时,设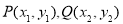 ,
,
联立 解得
解得
所以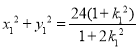 ,同理,得
,同理,得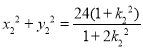 ,
,
由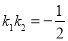 ,
,
所以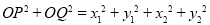
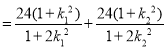

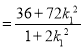
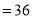
(ii)当直线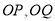 落在坐标轴上时,显然有
落在坐标轴上时,显然有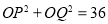 ,
,
综上: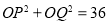 .
.
法二:(i)当直线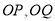 不落在坐标轴上时,设
不落在坐标轴上时,设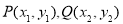 ,
,
因为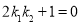 ,所以
,所以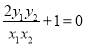 ,即
,即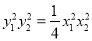 ,
,
因为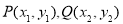 在椭圆C上,所以
在椭圆C上,所以 ,
,
即 ,
,
所以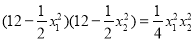 ,整理得
,整理得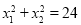 ,
,
所以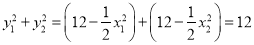 ,
,
所以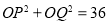 .
.
(ii)当直线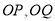 落在坐标轴上时,显然有
落在坐标轴上时,显然有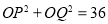 ,
,
综上: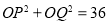 .
.
考点:1.直线与圆的位置关系;2.直线与椭圆的位置关系;3.定值问题.


科目:高中数学 来源:2014-2015学年辽宁沈阳东北育才学校高二上学期第二段考文科数学卷(解析版) 题型:选择题
抛物线y2= 2x的准线方程是
A.y=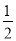 B.y=-
B.y=-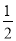 C.x=
C.x=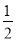 D.x=-
D.x=- 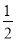
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省东莞市三校高二上学期期中联考试卷(解析版) 题型:选择题
若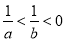 ,则下列不等式中,正确的不等式有 ( )
,则下列不等式中,正确的不等式有 ( )
①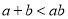 ②
②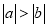 ③
③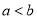 ④
④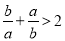
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上进教育名校学术联盟高三调研考试三文科数学试卷(解析版) 题型:选择题
已知变量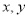 满足
满足 ,若目标函数
,若目标函数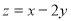 取到最大值为( )
取到最大值为( )
A.3 B.0 C.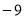 D.
D.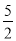
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省宿迁市高三上学期第一次摸底考试数学试卷(解析版) 题型:解答题
已知数列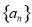 的各项均为正整数,对于任意n∈N*,都有
的各项均为正整数,对于任意n∈N*,都有 成立,且
成立,且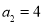 .
.
(1)求 ,
,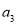 的值;
的值;
(2)猜想数列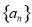 的通项公式,并给出证明.
的通项公式,并给出证明.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省宿迁市高三上学期第一次摸底考试数学试卷(解析版) 题型:填空题
在平面直角坐标系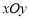 中,若双曲线的渐近线方程是
中,若双曲线的渐近线方程是 ,且经过点
,且经过点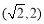 ,则该双曲线的方程是 .
,则该双曲线的方程是 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省杭州市高二11月月考数学试卷(解析版) 题型:选择题
在棱长为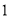 的正方体
的正方体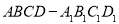 中,点
中,点 ,
,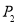 分别是线段
分别是线段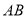 ,
,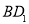 (不含端点)上的动点,且线段
(不含端点)上的动点,且线段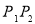 平行于平面
平行于平面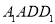 ,则四面体
,则四面体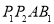 的体积的最大值为( )
的体积的最大值为( )
A.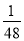 B.
B.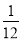 C.
C.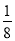 D.
D.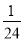
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com