练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知集合A={1，3，5，7}，B={x|（2x﹣1）（x﹣5）＞0}，则A∩（RB）（ ）
    A.{1，3}
    B.{1，3，5}
    C.{3，5}
    D.{3，5，7}

    【答案】B
    【解析】解：∵A={1，3，5，7}，

    B={x|（2x﹣1）（x﹣5）＞0}={x|x＜ 或x＞5}，

    ∴RB={x| }，

    则A∩（RB）={1，3，5}．

    所以答案是：B．

    【考点精析】根据题目的已知条件，利用交、并、补集的混合运算的相关知识可以得到问题的答案，需要掌握求集合的并、交、补是集合间的基本运算，运算结果仍然还是集合，区分交集与并集的关键是“且”与“或”，在处理有关交集与并集的问题时，常常从这两个字眼出发去揭示、挖掘题设条件，结合Venn图或数轴进而用集合语言表达，增强数形结合的思想方法．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知双曲线 的离心率为e，经过第一、三象限的渐近线的斜率为k，且e≥ k．
    （1）求m的取值范围；
    （2）设条件p：e≥ k；条件q：m2﹣（2a+2）m+a（a+2）≤0．若p是q的必要不充分条件，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校为了解1000名高一新生的身体生长状况，用系统抽样法（按等距的规则）抽取40名同学进行检查，将学生从1～1000进行编号，现已知第18组抽取的号码为443，则第一组用简单随机抽样抽取的号码为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱柱中， 平面， ， 在线段上， ， .

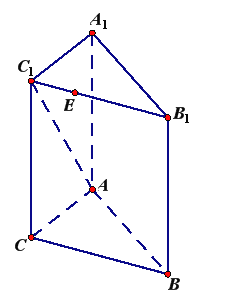
    （1）求证： ；

    （2）试探究：在上是否存在点，满足平面，若存在，请指出点的位置，并给出证明；若不存在，说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】田忌和齐王赛马是历史上有名的故事，设齐王的三匹马分别为，田忌的三匹马分别为 .三匹马各比赛一次，胜两场者为获胜.若这六匹马比赛的优劣程度可以用以下不等式表示： .

    （1）如果双方均不知道对方马的出场顺序，求田忌获胜的概率；

    （2）为了得到更大的获胜概率，田忌预先派出探子到齐王处打探实情，得知齐王第一场必出上等马，那么，田忌应怎样安排出马的顺序，才能使自己获胜的概率最大？最大概率是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】大西洋鲑鱼每年都要逆流而上，游回产地产卵，研究鲑鱼的科学家发现鲑鱼的游速（单位： ）与其耗氧量单位数之间的关系可以表示为函数，其中为常数，已知一条鲑鱼在静止时的耗氧量为100个单位；而当它的游速为时，其耗氧量为2700个单位.

    （1）求出游速与其耗氧量单位数之间的函数解析式；

    （2）求当一条鲑鱼的游速不高于时，其耗氧量至多需要多少个单位？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知正三棱柱， 是的中点．

    求证：（1）平面；

    （2）平面平面．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在三棱柱ABC﹣A1B1C1中，侧面ABB1A1为矩形，AB=2，AA1=2 ，D是AA1的中点，BD与AB1交于点O，且CO⊥平面ABB1A1 ．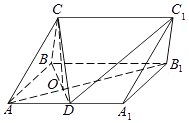

    （1）证明：CD⊥AB1；
    （2）若OC=OA，求直线CD与平面ABC所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f（x）=ex（sinx﹣cosx）（0≤x≤2016π），则函数f（x）的各极大值之和为（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    同步练习册答案