
分析 利用分离常数法求函数的值域.
解答 解:函数y=$\frac{\frac{1}{2}{e}^{x}-1}{{e}^{x}+1}$=$\frac{\frac{1}{2}({e}^{x}+1)-\frac{3}{2}}{{e}^{x}+1}$=$\frac{1}{2}$$-\frac{\frac{3}{2}}{{e}^{x}+1}$
∵x>-1,
∴${e}^{x}+1>\frac{1}{e}+1$
∴$\frac{\frac{3}{2}}{{e}^{x}+1}$<$\frac{3}{\frac{2}{e}+2}$
∴-$\frac{\frac{3}{2}}{{e}^{x}+1}$>-$\frac{3}{\frac{2}{e}+2}$.
∴y=$\frac{1}{2}$$-\frac{\frac{3}{2}}{{e}^{x}+1}$>$\frac{1}{2}$-$\frac{3}{\frac{2}{e}+2}$.
故得函数y的值域为($\frac{1}{2}-\frac{3e}{2+2e}$,$\frac{1}{2}$).
点评 本题考查了函数值域的求法.高中函数值域求法有:1、观察法,2、配方法,3、反函数法,4、判别式法;5、换元法,6、数形结合法,7、不等式法,8、分离常数法,9、单调性法,10、利用导数求函数的值域,11、最值法,12、构造法,13、比例法.要根据题意选择.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | sin($\frac{3π}{2}$+α)=cosα | B. | 常数数列一定是等比数列 | ||
| C. | 若0<a<$\frac{1}{b}$,则ab<1 | D. | x+$\frac{1}{x}$≥2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)在区间[a,b]上不可能有零点 | |
| B. | 函数f(x)在区间[a,b]上一定有零点 | |
| C. | 若函数f(x)在区间[a,b]上有零点,则必有f(a)•f(b)<0 | |
| D. | 若函数f(x)在区间[a,b]上没有零点,则必有f(a)•f(b)>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 960 | B. | -160 | C. | -560 | D. | -960 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数$f(x)=\frac{x+2}{x-2}$.
已知函数$f(x)=\frac{x+2}{x-2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
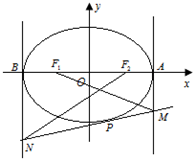 如图,已知椭圆$\frac{x^2}{4}$+$\frac{y^2}{3}$=1上任意一点P(异于顶点)处的切线与该椭圆在长轴顶点A,B处的切线分别交于点M,N,该椭圆的左,右焦点分别是F1,F2,直线MF1,NF2的斜率分别是k1,k2.
如图,已知椭圆$\frac{x^2}{4}$+$\frac{y^2}{3}$=1上任意一点P(异于顶点)处的切线与该椭圆在长轴顶点A,B处的切线分别交于点M,N,该椭圆的左,右焦点分别是F1,F2,直线MF1,NF2的斜率分别是k1,k2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com