
| 年份 | 11年 | 12年 | 13年 | 14年 | 15年 |
| 旅游节届编号x | 1 | 2 | 3 | 4 | 5 |
| 外地游客人数y(单位:十万) | 0.6 | 0.8 | 0.9 | 1.2 | 1.5 |
分析 (1)先求平均数,再将数据依次代入相关公式,求出$\widehatb=0.22$以及$\widehata=\overline y-\widehatb\overline x$=1-0.22×3=0.34;
(2)本题实际为利用线性回归方程进行估值:当x=7时,$\widehaty=0.22×7+0.34=1.88$,即得结果.
解答 解:(1)由所给数据计算得:$\overline x=\frac{1}{5}(1+2+3+4+5)=3$,$\overline y=\frac{1}{5}(0.6+0.8+0.9+1.2+1.5)=1$,$\sum_{i=1}^5{{{({x_i}-\overline x)}^2}=}4+1+0+1+4=10$,$\sum_{i=1}^5{({x_i}-\overline x)({y_i}-\overline y)=(-2)×}(-0.4)+(-1)×(-0.2)+0+1×0.2+2×0.5=2.2$,$\widehatb=\frac{2.2}{10}=0.22$,$\widehata=\overline y-\widehatb\overline x$=1-0.22×3=0.34,
所求的回归方程为$\widehaty=0.22x+0.34$.
(2)由(1)知,当x=7时,$\widehaty=0.22×7+0.34=1.88$,
于是预测2017年第七届中国柳州国际水上狂欢节到柳州的外地游客可达18万8千人.
点评 函数关系是一种确定的关系,相关关系是一种非确定的关系.事实上,函数关系是两个非随机变量的关系,而相关关系是非随机变量与随机变量的关系.如果线性相关,则直接根据用公式求a,


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0° | B. | 60° | C. | 30° | D. | 45° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
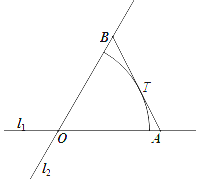 如图,在某商业区周边有两条公路l1和l2,在点O处交汇;该商业区为圆心角$\frac{π}{3}$、半径3km的扇形.现规划在该商业区外修建一条公路AB,与l1,l2分别交于A,B,要求AB与扇形弧相切,切点T不在l1,l2上.
如图,在某商业区周边有两条公路l1和l2,在点O处交汇;该商业区为圆心角$\frac{π}{3}$、半径3km的扇形.现规划在该商业区外修建一条公路AB,与l1,l2分别交于A,B,要求AB与扇形弧相切,切点T不在l1,l2上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某教育机构为了解本地区高三学生上网的情况,随机抽取了100名学生进行调查.下面是根据调查结果绘制的学生每天上网时间的频率分布直方图:将每天上网时间不低于40分钟的学生称为“上网迷”.
某教育机构为了解本地区高三学生上网的情况,随机抽取了100名学生进行调查.下面是根据调查结果绘制的学生每天上网时间的频率分布直方图:将每天上网时间不低于40分钟的学生称为“上网迷”.| 非上网迷 | 上网迷 | 合计 | |
| 男 | |||
| 女 | 10 | 55 | |
| 合计 |
| P(X2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com