
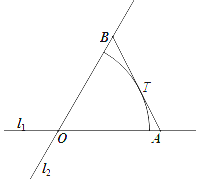
 如图,在某商业区周边有两条公路l1和l2,在点O处交汇;该商业区为圆心角$\frac{π}{3}$、半径3km的扇形.现规划在该商业区外修建一条公路AB,与l1,l2分别交于A,B,要求AB与扇形弧相切,切点T不在l1,l2上.
如图,在某商业区周边有两条公路l1和l2,在点O处交汇;该商业区为圆心角$\frac{π}{3}$、半径3km的扇形.现规划在该商业区外修建一条公路AB,与l1,l2分别交于A,B,要求AB与扇形弧相切,切点T不在l1,l2上.分析 (1)由余弦定理求出AB的长,建立直角坐标系,写出直线AB的方程,
利用AB与扇形弧相切d=r,得出a、b的关系式,再写出a、b的取值范围;
(2)根据OT⊥AB,求出AT、BT的值,写出AB的解析式,
利用三角函数与基本不等式求出它的最小值.
解答 解:(1)在△AOB中,OA=akm,OB=bkm,$∠AOB=\frac{π}{3}$;
由余弦定理得:
$A{B^2}=O{A^2}+O{B^2}-2OA•OBcos∠AOB={a^2}+{b^2}-2abcos\frac{π}{3}$=a2+b2-ab;
所以$AB=\sqrt{{a^2}+{b^2}-ab}$;…(2分)
如图,以O为原点,OA所在直线为x轴,建立直角坐标系,
则$A(a,0),B(\frac{1}{2}b,\frac{{\sqrt{3}}}{2}b)$,
所以直线AB的方程为$y=\frac{{\frac{{\sqrt{3}}}{2}b}}{{\frac{1}{2}b-a}}(x-a)$,
即$\sqrt{3}bx+(2a-b)y-\sqrt{3}ab=0$; …(4分)
因为AB与扇形弧相切,所以$\frac{{\sqrt{3}ab}}{{\sqrt{3{b^2}+{{(2a-b)}^2}}}}=3$,
即${a^2}+{b^2}=\frac{1}{12}{a^2}{b^2}+ab$; a,b∈(3,6)…(6分)
(2)因为OT是圆O的切线,所以OT⊥AB.
在Rt△OTA中,AT=3tanα;
在Rt△OTB中,$BT=3tan(\frac{π}{3}-α)$;
所以,AB=AT+TB=3tanα+3tan($\frac{π}{3}$-α)(0<α<$\frac{π}{3}$); …(9分)
所以,AB=3(tanα+$\frac{\sqrt{3}-tanα}{1+\sqrt{3}tanα}$)=$3\sqrt{3}\;\frac{{{{tan}^2}α+1}}{{1+\sqrt{3}tanα}}$; …(12分)
设$1+\sqrt{3}tanα=u$,u∈(1,4),
则$AB=3\sqrt{3}\;\frac{{{{(\frac{u-1}{{\sqrt{3}}})}^2}+1}}{u}=\sqrt{3}\;(u+\frac{4}{u}-2)≥\sqrt{3}•2=2\sqrt{3}$,
当且仅当u=2,即$α=\frac{π}{6}$时取等号;
此时$OA=OB=2\sqrt{3}$km.
所以,当$OA=OB=2\sqrt{3}$km时,新建公路AB的长度最短. …(16分)
点评 本题考查了三角函数模型的应用问题,也考查了三角恒等变换以及求值问题,是综合题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f′(x0) | B. | -f′(x0) | C. | -2f′(x0) | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 11年 | 12年 | 13年 | 14年 | 15年 |
| 旅游节届编号x | 1 | 2 | 3 | 4 | 5 |
| 外地游客人数y(单位:十万) | 0.6 | 0.8 | 0.9 | 1.2 | 1.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\left\{{\begin{array}{l}{x=3x'}\\{y=\frac{1}{2}y'}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{x'=3x}\\{y'=\frac{1}{2}y}\end{array}}\right.$ | C. | $\left\{{\begin{array}{l}{x=3x'}\\{y=2y'}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{x'=3x}\\{y'=2y}\end{array}}\right.$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 0个 | C. | 2个 | D. | 无数个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com