
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 根据q=1或q≠1,判断,
根据等比数列的性质判断
利用等比数列的特例判断.
解答 解:{an}是首项为a1,公比为q的等比数列,Sn是{an}的前n项和
若q=1,则Sn=n,若q≠1,则Sn=$\frac{{a}_{1}(1-{q}^{n})}{1-q}$,故错误,
若am•an=as•at,则m+n=s+t,故错误
设an=(-1)n,
则S2=0,S4-S2=0,S6-S4=0,
∴此数列不是等比数列,故Sk,S2k-Sk,S3k-S2k(k为常数且k∈N)不一定是等比数列说法错误,
故以上说法正确的有0个,
故选:A.
点评 本题考查命题的真假判断,考查数列的性质,正确命题要严格注明,错误命题列举反例即可.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
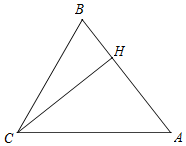 已知三角形△ABC中,∠ACB=60°,CH为AB边上的高,H为垂足;设BC=a,CA=b,AB=c,CH=h;
已知三角形△ABC中,∠ACB=60°,CH为AB边上的高,H为垂足;设BC=a,CA=b,AB=c,CH=h;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com