
【题目】下列命题中,m,n表示两条不同的直线,![]() 、
、![]() 、
、![]() 表示三个不同的平面.正确的命题是( )
表示三个不同的平面.正确的命题是( )
![]() 若
若![]() ,
,![]() ,则
,则![]() ;
;![]() 若
若![]() ,
,![]() ,则
,则![]() ;
;
![]() 若
若![]() ,
,![]() ,则
,则![]() ;
;![]() 若
若![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】设函数![]() 的定义域为
的定义域为![]() ,若存在常数
,若存在常数![]() ,使
,使![]() 对一切实数
对一切实数![]() 均成立,则称
均成立,则称![]() 为“倍约束函数”
为“倍约束函数”![]() 现给出下列函数:
现给出下列函数:![]() ;
;![]() ;
;![]() ;
;![]() 是定义在实数集
是定义在实数集![]() 上的奇函数,且对一切
上的奇函数,且对一切![]() ,
,![]() 均有
均有![]() 其中是“倍约束函数”的序号是
其中是“倍约束函数”的序号是![]()
![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() 为参数),直线
为参数),直线![]() 经过点
经过点![]() ,且倾斜角为
,且倾斜角为![]() .
.
(1)写出直线![]() 的参数方程和圆
的参数方程和圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,我国电子商务蓬勃发展,有关部门推出了针对网购平台的商品和服务的评价系统,从该系统中随机选出100次成功了的交易,并对这些交易的评价进行统计,网购者对商品的满意率为0.6,对服务的满意率为0.75,其中对商品和服务都满意的交易为40次.
(1)根据已知条件完成下面的![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“网购者对服务满意与对商品满意之间有关”?
的把握认为“网购者对服务满意与对商品满意之间有关”?

(2)若将频率视为概率,某人在该网购平台上进行的3次购物中,设对商品和服务都满意的次数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:  (其中
(其中![]() 为样本容量)
为样本容量)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网店统计了连续三天售出商品的种类情况:第一天售出19种商品,第二天售出13种商品,第三天售出18种商品;前两天都售出的商品有3种,后两天都售出的商品有4种,则该网店
①第一天售出但第二天未售出的商品有______种;
②这三天售出的商品最少有_______种.
查看答案和解析>>
科目:高中数学 来源: 题型:
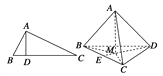
【题目】如图,在△ABC中,AB⊥AC,若AD⊥BC,则AB2=BD·BC;类似地有命题:在三棱锥A-BCD中,AD⊥平面ABC,若A点在平面BCD内的射影为M,则有S![]() =S△BCM·S△BCD.上述命题是 ( )
=S△BCM·S△BCD.上述命题是 ( )
A. 真命题
B. 增加条件“AB⊥AC”才是真命题
C. 增加条件“M为△BCD的垂心”才是真命题
D. 增加条件“三棱锥A-BCD是正三棱锥”才是真命题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com