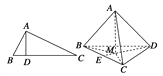
【题目】如图，在△ABC中，AB⊥AC，若AD⊥BC，则AB2＝BD·BC；类似地有命题：在三棱锥A－BCD中，AD⊥平面ABC，若A点在平面BCD内的射影为M，则有S＝S△BCM·S△BCD.上述命题是 (　　)

A. 真命题

B. 增加条件“AB⊥AC”才是真命题

C. 增加条件“M为△BCD的垂心”才是真命题

D. 增加条件“三棱锥A－BCD是正三棱锥”才是真命题

参考答案：

【答案】A

【解析】因为AD⊥平面ABC，AE平面ABC，BC 平面ABC，

所以AD⊥AE，AD⊥BC．

在△ADE中，AE2＝ME·DE，

又A点在平面BCD内的射影为M，

所以AM⊥平面BCD，AM⊥BC，

所以BC⊥平面ADE，

所以BC⊥DE，BC⊥AE．

又，

所以．选A．

关闭