设Sn是等比数列{an}的前n项和.S4=5S2.则此数列的公比q=( )A．-2或-1B．1或2C．±1或2D．±2或-1 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

2．设S_n是等比数列{a_n}的前n项和，S₄=5S₂，则此数列的公比q=（　　）

A．

-2或-1

B．

1或2

C．

±1或2

D．

±2或-1

分析对q分类讨论，利用等比数列的求和公式即可得出．

解答解：q=1时不满足条件，舍去．
q≠1时，∵S₄=5S₂，则$\frac{{a}_{1}（1-{q}^{4}）}{1-q}$=$\frac{5{a}_{1}（1-{q}^{2}）}{1-q}$，
∴1-q⁴=5（1-q²），
∴（q²-1）（q²-4）=0，q≠1，
解得q=-1，或±2．
故选：D．

点评本题考查了等比数列的求和公式，考查了分类讨论方法、推理能力与计算能力，属于中档题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：填空题

17．已知圆C：x²+y²+2kx+2y+k²=0（k∈R）和定点P（1，-1），若过P点可以作两条直线与圆C相切，则k的取值范围是（0，+∞）∪（-∞，-2）．．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

13．用描述法表示图中阴影部分的点（含边界）的坐标的集合为{（x，y）|xy＞0，且-1≤x≤2，-$\frac{1}{2}$≤y≤1}．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

10．

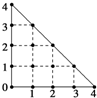某人在如图所示的直角边长为4米的三角形地块的每个格点（指纵、横直线的交叉点以及三角形的顶点）处都种了一株相同品种的作物．根据历年的种植经验，一株该种作物的年收获量Y（单位：kg）与它的“相近”作物株数X之间的关系如表所示：

X	1	2	3	4
Y	51	48	45	42

这里，两株作物“相近”是指它们之间的直线距离不超过1米．
（1）完成下表，并求所种作物的平均年收获量：

Y	51	48	45	42
频数

（2）在所种年收获量为51或48的作物中随机选取两株求收获量之和，收获量之和为t的概率．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

17．探究函数f（x）=2x+$\frac{8}{x}$，x∈（0，+∞）最小值，并确定取得最小值时x的值．列表如下：

x	…	0.5	1	1.5	1.7	1.9	2	2.1	2.2	2.3	3	4	5	7	…
y	…	17	10	8.34	8.1	8.01	8	8.01	8.04	8.08	8.6	10	11.6	15.14	…

请观察表中y值随x值变化的特点，完成以下的问题．
（1）函数f（x）=2x+$\frac{8}{x}$（x＞0）在区间（0，2）上递减；函数f（x）=2x+$\frac{8}{x}$（x＞0）在区间（2，+∞）上递增．当x=2时，y_最小=8．
（2）证明：函数f（x）=2x+$\frac{8}{x}$（x＞0）在区间（0，2）递减．
（3）思考：函数f（x）=2x+$\frac{8}{x}$（x＜0）时，有最值吗？是最大值还是最小值？此时x为何值？（直接回答结果，不需证明）

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

7．已知数列{a_n}的前n项和S_n=n²-4n．
（1）求数列{a_n}的通项公式；
（2）求S_n的最大或最小值．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

14．函数f（x）=$\left\{\begin{array}{l}{1-{x}^{2}，x≤1}\\{lnx，x＞1}\end{array}\right.$，若方程f（x）=mx-$\frac{1}{3}$恰有四个不等的实数根，则实数m的取值范围是（$\frac{1}{3}$，${e}^{-\frac{2}{3}}$）．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

11．已知函数f（x）=$\frac{1}{2}$x²-2ax+blnx+2a²在x=1处取得极值$\frac{1}{2}$，则a+b=（　　）

A．

-1

B．

C．

-1或1

D．

-1或2

查看答案和解析>>

科目：高中数学 来源： 题型：选择题