练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

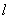    已知直线过点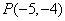，且与两坐标轴围成的三角形的面积为5，求直线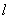的方程.

    改编：过点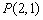作直线l分别交x、y正半轴于A、B两点，

    （1）当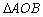面积最小时，直线l的方程为____________；

    （2）当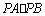最小时，直线l的方程为____________．


    （1）

        （2）

    [解析] 法一：由题意斜率存在，可设直线方程为

    令；令.所以，

    当且仅当时取等号，此时直线方程为.

    法二：由题意截距不为0，可设直线方程为，

    过点，有，所以，解得，

    所以，此时，即


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知集合M＝{1，－2,3}，N＝{－4,5,6，－7}，从两个集合中各取一个元素作为点的坐标，则在直角坐标系中，第一、第二象限不同点的个数是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    三边长均为整数，且最大边长为11的三角形个数是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若x＝，则x＝______________.(用排列数表示)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    判断下列问题是否为排列问题：

    (1)北京、上海、天津三个民航站之间的直达航线的飞机票的价格(假设来回的票价相同)；

    (2)选2个小组分别去植树和种菜；

    (3)选2个小组去种菜；

    (4)选10人组成一个学习小组；

    (5)选3个人分别担任班长、学习委员、生活委员；

    (6)某班40名学生在假期相互通信．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如果圆上总存在两个点到原点的距离为1，则实数的取值范围____________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知全集为R，集合A＝，B＝，则A∩∁RB＝________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    对任意整数，函数满足，若，则         ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     “求方程的解”有如下解题思路：设，则在R上单调递减，且，所以原方程有唯一解。类比上述解题思路，不等式的解集为________.

    查看答案和解析>>

    同步练习册答案