
���� ��1��ֱ�Ӵ�����㼴�ɣ�
��2��ͨ���۲��֪an+1=2an+��1+3��•2n-1����������ͬʱ����2n+1�������ɵ�����{$\frac{{a}_{n}}{{2}^{n}}$}����������Ϊ1�ĵȲ����У����㼴�ý��ۣ�
��3��ͨ����2�������֪$\frac{{a}_{n+2}}{{a}_{n}{a}_{n+1}}$=4[$\frac{1}{n•{2}^{n}}$-$\frac{1}{��n+1��•{2}^{n+1}}$]������������Ӽ��ý��ۣ�
��� �⣺��1�������⣬a3=4+6+6+8=24��
a4=5+7+7+9+7+9+9+11=64��
a5=6+8+8+10+8+10+10+12+8+10+10+12+10+12+12+14=160��
��2���ߴӵڶ�������һ�е�����ÿһ�����1д�����ٸ����ټ�3д����
��an+1=2an+��1+3��•2n-1����an+1=2an+2n+1��
����ͬʱ����2n+1���ã�$\frac{{a}_{n+1}}{{2}^{n+1}}$=$\frac{{a}_{n}}{{2}^{n}}$+1��
�֡�$\frac{{a}_{1}}{{2}^{1}}$=1��
��$\frac{{a}_{n}}{{2}^{n}}$=n����an=n•2n��
��3���ɣ�2����֪$\frac{{a}_{n+2}}{{a}_{n}{a}_{n+1}}$=$\frac{��n+2��•{2}^{n+2}}{n��n+1��•{2}^{n}•{2}^{n+1}}$=4[$\frac{1}{n•{2}^{n}}$-$\frac{1}{��n+1��•{2}^{n+1}}$]��
��Sn=$\frac{{a}_{3}}{{a}_{1}{a}_{2}}$+$\frac{{a}_{4}}{{a}_{2}{a}_{3}}$+��+$\frac{{a}_{n+2}}{{a}_{n}{a}_{n+1}}$
=4[$\frac{1}{1•{2}^{1}}$-$\frac{1}{2•{2}^{2}}$+$\frac{1}{2•{2}^{2}}$-$\frac{1}{3•{2}^{3}}$+��+$\frac{1}{n•{2}^{n}}$-$\frac{1}{��n+1��•{2}^{n+1}}$]
=4[$\frac{1}{1•{2}^{1}}$-$\frac{1}{��n+1��•{2}^{n+1}}$]
=2-$\frac{1}{��n+1��•{2}^{n-1}}$��n��N*����
��$\underset{lim}{n����}$Sn=$\underset{lim}{n����}$[2-$\frac{1}{��n+1��•{2}^{n-1}}$]=2��
���� ���⿼�����е�ͨ�ǰn��ͣ�����������������������������������Ա���ʽ���������ǽ������Ĺؼ���ע����ⷽ���Ļ��ۣ������е��⣮


 �¿α�������������ҵ�������γ�����ϵ�д�
�¿α�������������ҵ�������γ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
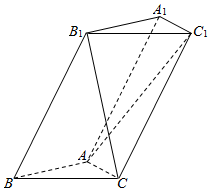 ��ͼ��������ABC-A1B1C1�У�����ABCΪ����ֱ�������Σ�AB=AC=1��BB1=2����ABB1=60�㣮
��ͼ��������ABC-A1B1C1�У�����ABCΪ����ֱ�������Σ�AB=AC=1��BB1=2����ABB1=60�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 3 | C�� | 5 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | $\sqrt{5}$ | C�� | 5 | D�� | $\frac{{\sqrt{50}}}{3}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com