
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | $\frac{3}{2}$ |
分析 结合题意设出$\overrightarrow{a}$,$\overrightarrow{b}$的坐标,求出$\overrightarrow{a}$-2$\overrightarrow{b}$的坐标,从而求出$\overrightarrow{a}$-2$\overrightarrow{b}$的模即可.
解答 解:平面向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为$\frac{π}{3}$,且|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=$\frac{1}{2}$,
不妨设$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=($\frac{1}{4}$,$\frac{\sqrt{3}}{4}$),
则$\overrightarrow{a}$-2$\overrightarrow{b}$=($\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$),
故|$\overrightarrow{a}$-2$\overrightarrow{b}$|=$\sqrt{\frac{1}{4}+\frac{3}{4}}$=1,
故选:A.
点评 本题考查了向量求模问题,考查向量的坐标运算,是一道基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
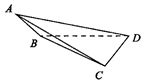 把平面图形M上的所有点在一个平面上的射影构成的图形M′叫作图形M在这个平面上的射影.如图,在三棱锥A-BCD中,BD⊥CD,AB⊥DB,AC⊥DC,AB=DB=5,CD=4,将围成三棱锥的四个三角形的面积从小到大依次记为S1,S2,S3,S4,设面积为S2的三角形所在的平面为α,则面积为S4的三角形在平面α上的射影的面积是( )
把平面图形M上的所有点在一个平面上的射影构成的图形M′叫作图形M在这个平面上的射影.如图,在三棱锥A-BCD中,BD⊥CD,AB⊥DB,AC⊥DC,AB=DB=5,CD=4,将围成三棱锥的四个三角形的面积从小到大依次记为S1,S2,S3,S4,设面积为S2的三角形所在的平面为α,则面积为S4的三角形在平面α上的射影的面积是( )| A. | 2$\sqrt{34}$ | B. | $\frac{25}{2}$ | C. | 10 | D. | 30 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(π)<f(3)<f($\sqrt{2}$) | B. | f(π)<f($\sqrt{2}$)<f(3) | C. | f($\sqrt{2}$)<f(3)<f(π) | D. | f($\sqrt{2}$)<f(π)<f(3) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
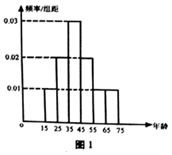 持续性的雾霾天气严重威胁着人们的身体健康,汽车的尾气排放是造成雾霾天气的重要因素之一.为此,某城市实施了机动车尾号限行,该市报社调查组为了解市区公众对“车辆限行”的态度,随机选取了30人进行调查,将他们的年龄(单位:岁)数据绘制成频率分布直方图(图1),并将调查情况进行整理后制成表2:
持续性的雾霾天气严重威胁着人们的身体健康,汽车的尾气排放是造成雾霾天气的重要因素之一.为此,某城市实施了机动车尾号限行,该市报社调查组为了解市区公众对“车辆限行”的态度,随机选取了30人进行调查,将他们的年龄(单位:岁)数据绘制成频率分布直方图(图1),并将调查情况进行整理后制成表2:| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
| 频数 | 3 | 6 | 6 | 3 | ||
| 赞成人数 | 2 | 4 | 5 | 4 | 2 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{c}$ | B. | $\frac{1}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{3}$$\overrightarrow{c}$ | C. | $\frac{1}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{6}$$\overrightarrow{c}$ | D. | $\frac{1}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$-$\frac{1}{4}$$\overrightarrow{c}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com